機械学習で準結晶を形成する化学組成を同定 準結晶の安定化メカニズムの解明に向けた第一歩
ISM2021-07
2021年7月20日
概要
準結晶は通常の結晶のような並進対称性を持たないが、原子配列に高度な秩序がある物質群です(※1)。最初の準結晶は1984年にイスラエルの冶金学者ダニエル・シェヒトマン博士(Daniel Shechtman)によって発見されました。その後およそ35年間で約100個の熱力学的に安定な準結晶が見つかり、準結晶は新しい固体構造の概念として確立されました。しかしながら、近年は準結晶の発見のペースが著しく鈍化しています。
統計数理研究所、東京大学、東京理科大学の共同研究グループは、機械学習のアルゴリズムを駆使してこれまでに見つかった準結晶の組成パターンを読み解き、新しい準結晶の化学組成を予測できることを実証しました。さらに、機械学習のブラックボックスモデルに内在する入出力のルールを抽出することで、準結晶相の形成に関する法則を明らかにしました。この法則は五つの単純な数式で表されます。これらは、準結晶研究において長年求められてきた物質探索の設計指針になる可能性があります。
本研究成果は、2021年7月19日に国際学術誌「Advanced Materials」にオンライン掲載されました。
1.背景
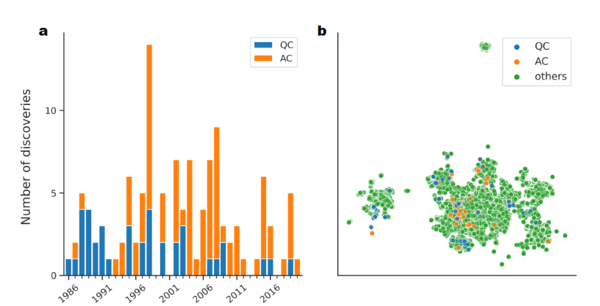
準結晶は、通常の結晶のような並進対称性はないが、原子の配列に高い秩序性がある物質です。最初の準結晶は1984年にイスラエルの冶金学者ダニエル・シェヒトマン博士(2011年にノーベル化学賞を受賞)によって発見されました。それ以降、これまでに100個ほどの安定準結晶が見つかってきました。準結晶研究の歴史の中で、新しい準結晶の発見は、電子物性の異常、絶縁体的な振る舞い、価数揺らぎ、量子臨界性、超伝導などの新しい物理現象の発見をもたらしてきました。しかしながら、近年は新しい準結晶の発見のペースは著しく低下しています(図1)。このような傾向は、新しい安定準結晶を合成するための明確な設計指針が確立されていないことが主な原因です。
|
|
|
図 1. これまでに発見されたアルミニウム合金の安定準結晶。(a) 準結晶(QC)と近似結晶(AC)の発見数の年推移。(b)これまでに見つかった準結晶・近似結晶・周期結晶を含むその他(others)の組成パターンの2次元平面への可視化。 |
2. 準結晶の組成予測
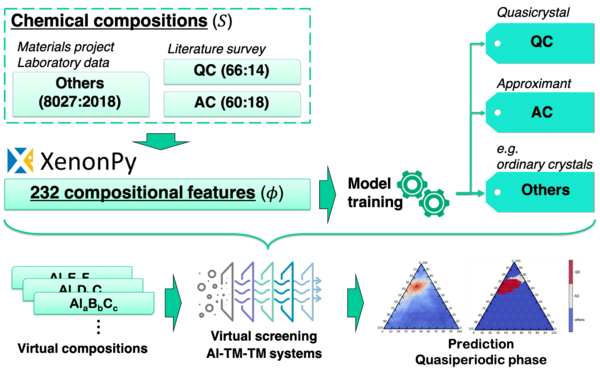
準結晶研究への機械学習の応用は、依然としてほぼ未踏領域です。機械学習は準結晶の発見に貢献できるのか。この問いに答えることが本研究の出発点でした。本研究グループは、非常に単純な機械学習のアプローチで準結晶を予測することに取り組みました(図2)。データ解析には、統計数理研究所ものづくりデータ科学研究センターの研究グループが開発しているオープンソースソフトウェアXenonPy(※2)を導入しました。モデルの入力変数は化学組成、出力変数は、“準結晶”、“近似結晶”、通常の周期結晶を含む“その他”を表すクラスラベルです。近似結晶は、準結晶と類似した局所構造を持つ準結晶の関連物質です。近似結晶は準結晶の組成の近くで形成されることが知られています。したがって、両者の安定化メカニズムはよく似ていると予想されています。学習データには、これまでに発見された準結晶、近似結晶、通常の周期結晶の化学組成を用いました。このデータで訓練したモデルの3クラス分類問題における予測能力を系統的に調べました。アルミニウムを含む三元合金系を対象に予測された準結晶相を実験相図と比較したところ、予測精度は約0.728に達することが分かりました。特に、通常の周期結晶はほぼ完ぺきに予測できることが判明しました。このアプローチを用いて、準結晶や近似結晶の候補組成を絞り込めば、物質探索の効率が大幅に向上することが期待されます。
|
|
| 図 2. 機械学習(3クラス分類問題)のワークフロー。モデルの入力変数は化学組成(S)、出力は準結晶(QC)、近似結晶(AC)、周期結晶を含むその他(”Others”)を表すクラスラベル |
3. 機械学習によるヒューム=ロザリー電子濃度則の再発見
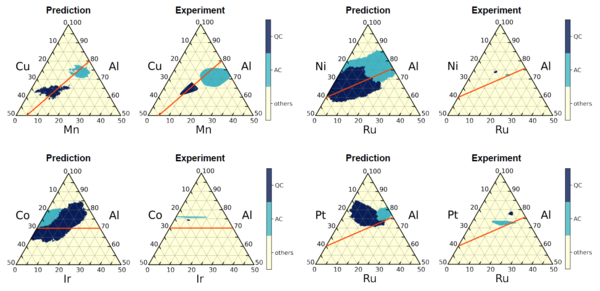
ここで、同グループは一つの興味深い事実に気付きました。機械学習のモデルは、ヒューム=ロザリーの電子濃度則という準結晶合金の形成に関する経験則を学習していることが分かりました。準結晶・近似結晶の多くは、1 原子当りの平均遍歴電子数e/a(※3)が特定の値をとる組成で安定化することが知られています。アルミニウム合金では、e/a = 1.8を満たす組成で安定な準結晶・近似結晶が形成されると言われています。図3に示すように、機械学習が予測した準結晶と近似結晶の領域は、ほとんどのアルミニウム合金において、e/a = 1.8の直線と重なっていることが分かりました。これは、機械学習のアルゴリズムがこれまでに発見された準結晶・近似結晶の組成データのみから、この広く知られた経験則を再発見したことを意味します。
|
|
| 図3.三元系アルミニウム合金の予測相図と実験相図との比較。紺が準結晶で、水色が近似結晶を表す。オレンジは平均遍歴電子数のヒューム=ロザリー則e/a=1.8を満たす直線を表す。 |
4. 準結晶の形成ルールの発見
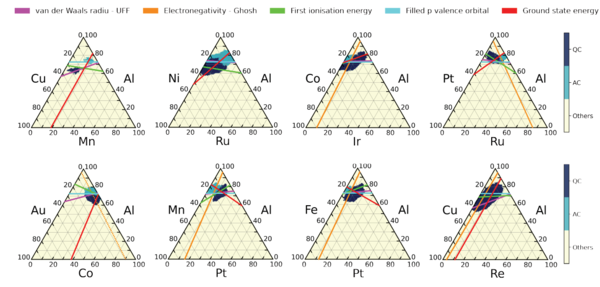
さらに同グループは、機械学習のブラックボックスモデルに内在する入出力のルールを抽出することで、準結晶と近似結晶の相形成に関する法則を明らかにしました。この法則は、原子のファンデルワールス半径(※4)や電気陰性度(※5)などに関する五つの単純な数式で表されます(図4)。これらの条件は、準結晶研究において長年求められてきた新しい準結晶を探索するための設計指針となります。また、モデルには他にも多くのルールが隠されている可能性があります。機械学習のブラックボックスモデルに埋め込まれたルールセットを網羅的に調べることで、準結晶の形成メカニズムを解き明せる可能性が明らかになりました。この成果をもとに固体物理学の中心課題である準結晶の安定化メカニズムを解明することを目指します。
|
|
| 図4. 機械学習による準結晶の形成ルールの発見。8種類の三元系に対する機械学習の予測相図(紺:準結晶、水色:近似結晶)。直線は機械学習が同定した五つのルールを表す。これらの合流点に準結晶相が現れる。 |
5. 今後の展開:革新的な準結晶の発見に向けて
今回の研究によって、我々はデータ科学による準結晶の発見を実現するための第一歩を踏み出しました。現在、この予測モデルを用いて、多くの研究者が新しい準結晶の合成に取り組んでいます。特に、半導体準結晶、超伝導準結晶、強磁性準結晶などの革新性の高い準結晶の発見を目指しています。データ科学を技術的な駆動力として準結晶の発見プロセスを加速する。今回の成果は、そのための第一歩です。1984年に初めて準結晶が発見されてから35年以上経過したにもかかわらず、準結晶の形成条件や安定化のメカニズムはほとんど分かっていません。データ科学が準結晶研究の未解決問題の解決に大きく貢献できるかもしれません。
掲載論文
題目:Machine learning to predict quasicrystals from chemical compositions
著者:Chang Liu1, Erina Fujita2, Yukari Katsura2, Yuki Inada2, Asuka Ishikawa3, Ryuji Tamura3, Kaoru Kimura2, Ryo Yoshida1,4,5
雑誌:Advanced Materials
DOI:10.1002/adma.202102507
(掲載日時:2021年7月19日)
1 The Institute of Statistical Mathematics, Research Organization of Information and Systems
2 The University of Tokyo, Graduate School of Frontier Sciences, Department of Advanced Materials Science
3 Tokyo University of Science, Department of Materials Science and Technology
4 Graduate University for Advanced Studies, Department of Statistical Science
5 Research and Services Division of Materials Data and Integrated System (MaDIS), National Institute for Materials Science (NIMS)
用語説明
※1 準結晶:周期結晶、アモルファスと並ぶ固体の三存在形態の一つです。二百数十年前から1984年までは、原子が周期的に配列した結晶と不規則に並んだアモルファスの二分類しかありませんでした。ところが、原子が規則的ではあるが周期を持たずに並んだ構造が発見され、準結晶と名付けられました。周期性の制約がないために、周期結晶では許されない5回対称性や、正20面体対称性などの回転対称性を持ち得ます。その後、主に金属間化合物で多く見つかってきましたが、最近は高分子や酸化物でも見つかり、固体構造の普遍的な概念になりました。
※2 XenonPy:マテリアルズインフォマティクスのオープンソースプラットフォーム
https://github.com/yoshida-lab/XenonPy
※3 平均遍歴電子数:s軌道やp軌道の価電子は、広がった波動関数を持ち伝導に大きく寄与します。一方、d軌道の価電子は波動関数が局在的で伝導に寄与し難く、しかも最外殻のd軌道に空きがあるとs軌道やp軌道の価電子が落ち込み伝導に寄与できる遍歴電子数が減ってしまうため、遷移金属元素の遍歴電子数は空いている軌道に収容できる電子数にマイナスを付けたものとして考えます。典型元素の価電子数に等しい遍歴電子数と、遷移金属元素のマイナスの遍歴電子数を平均したものが平均遍歴電子数です。
※4 ファンデルワールス半径:二つの非結合原子間の静電力のバランスが取れている場合、それらの間の距離の半分に等しくなります。提唱者ファン・デル・ワールス (Van der Waals) の名前からこの名が付きました。
※5 電気陰性度:原子核が電子を引き寄せる力の強さを表します。
謝辞
本研究は、文部科学省科学研究費補助金新学術領域研究「ハイパーマテリアル:補空間が創る新物質科学」(19H05820)の助成を受けました。
| お問い合わせ先 |
|
【研究内容について】
【報道・広報について】 |
プレスリリースpdf版はこちら
プレスリリース
- ISM2014-01
- ISM2014-02
- ISM2014-03
- ISM2014-04
- ISM2014-05
- ISM2014-06
- ISM2015-01
- ISM2015-02
- ISM2015-03
- ISM2015-04
- ISM2016-01
- ISM2016-02
- ISM2016-03
- ISM2016-04
- ISM2016-05
- ISM2016-06
- ISM2016-07
- ISM2016-08
- ISM2016-09
- ISM2016-10
- ISM2017-01
- ISM2017-02
- ISM2017-03
- ISM2017-04
- ISM2017-05
- ISM2018-01
- ISM2018-02
- ISM2018-03
- ISM2018-04
- ISM2018-05
- ISM2018-06
- ISM2018-07
- ISM2018-08
- ISM2019-01
- ISM2019-02
- ISM2019-03
- ISM2019-04
- ISM2019-05
- ISM2019-06
- ISM2019-07
- ISM2019-08
- ISM2019-09
- ISM2020-01
- ISM2020-02
- ISM2020-03
- ISM2020-04
- ISM2020-05
- ISM2020-06
- ISM2020-07
- ISM2020-08
- ISM2020-09
- ISM2020-10
- ISM2020-11
- ISM2020-12
- ISM2021-01
- ISM2021-02
- ISM2021-03
- ISM2021-04
- ISM2021-05
- ISM2021-06
- ISM2021-07