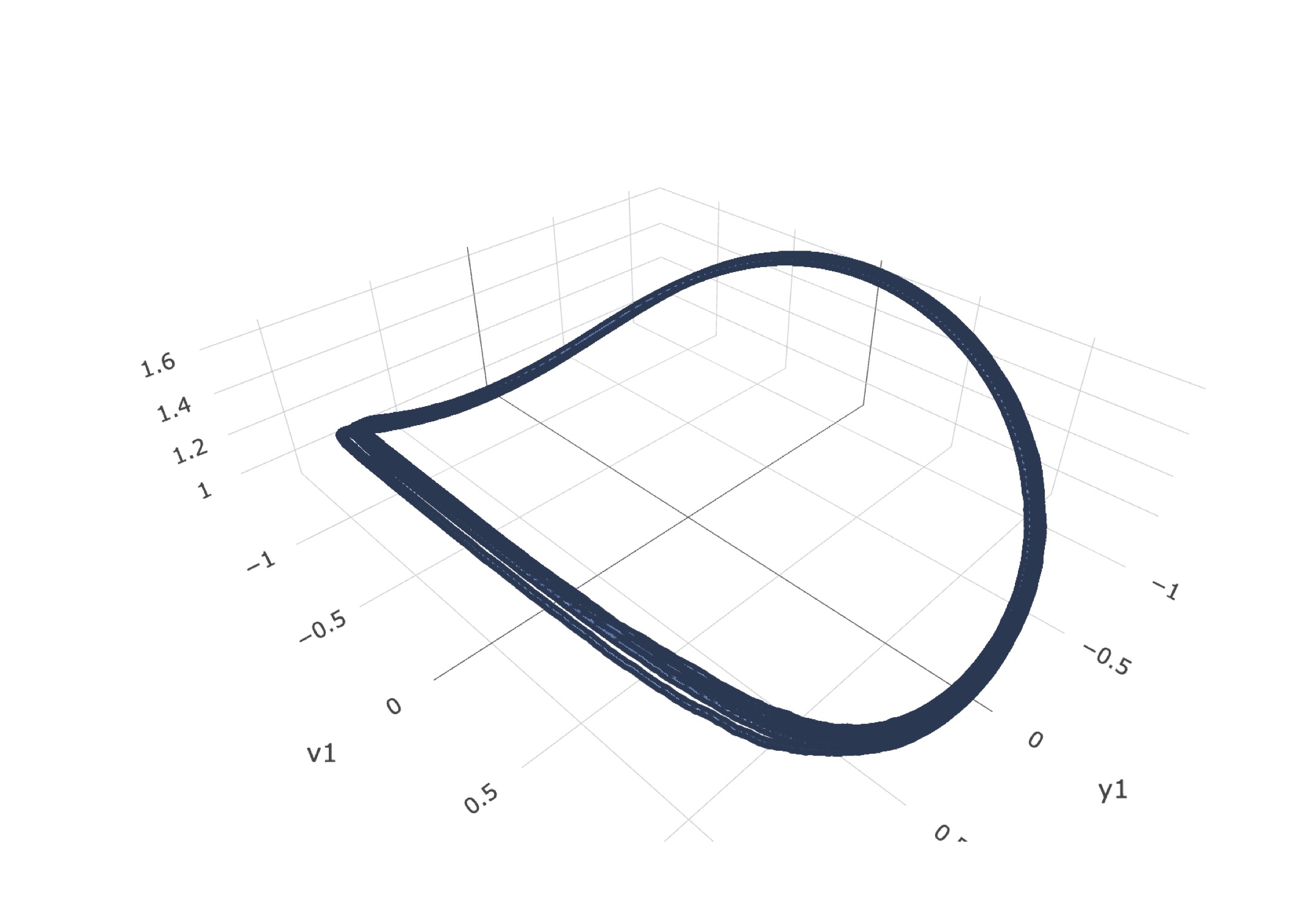
ベイズ統計を用いた金融時系列の定量的解析に取り組んでいます。ベ イズ統計的理解によって、結果の統一的解釈を実現し、金融時系列の パターンやダイナミクスに深い洞察を得ることができます。ただし、ベイ ズ統計の利用は計算的な困難を増やします。区分確定的マルコフ過程 を利用したスケーラブルな計算方法などの数理的解析や新手法の開発 によって計算効率と精度をともに高め、 金融分析の進歩に貢献しています。

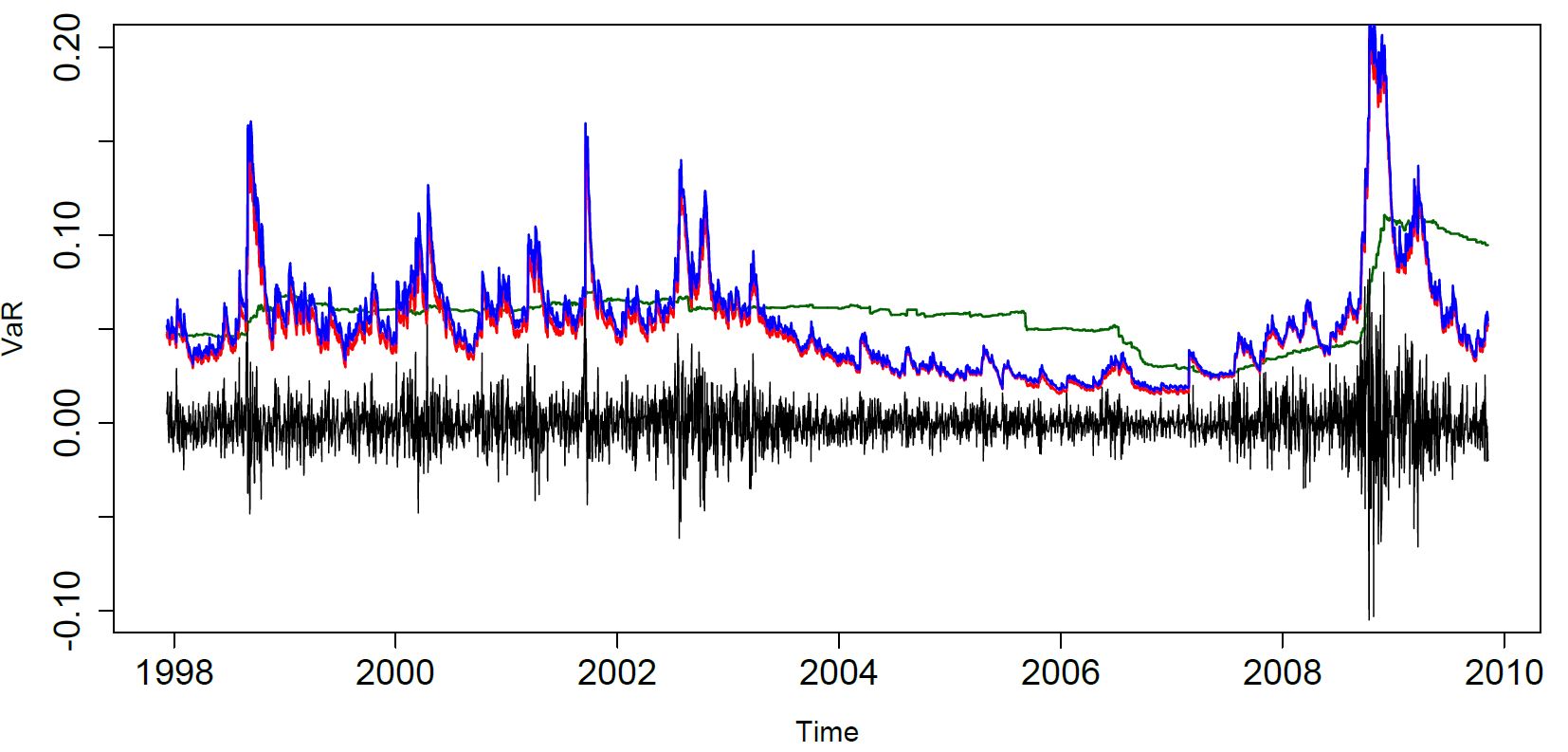
時系列モデルと極値理論の種々の組合せによる 損失率の99.9% 分位点の外挿予測

市場リスク管理では、資産価格の変動で極端に大きな損失 が生じるリスクを、例えば損失分布の上側1 % 点に対応す る分位点を推定することで把握し、予測に用います。典型 的には、損失率にGARCH モデル等の時系列モデルをあて はめて外挿予測を行いますが、更に統計的極値理論を組み 合わせることで、より高精度な高分位点予測が可能となり、 巨額損失の発生という稀少事象への統計モデルの対応能 力を高めることができます。

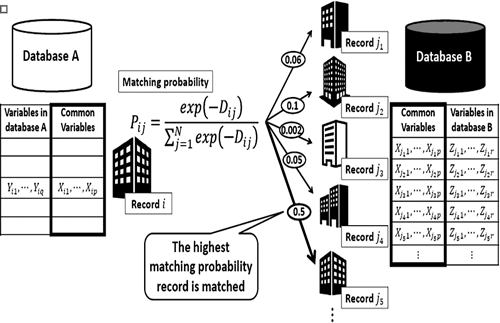多項ロジットモデルを利用した確率的名寄せ

銀行は企業の返済能力を自行で収集したデータを元に、統計モデル を作成し企業の信用力を評価してきましたが、インターネット上の情報 や政府の統計データ、信用調査会社のデータなど様々なデータが利 用可能となり、多くのデータベースを統合することが重要となりました。 その際、確率的名寄せの方法、欠損フィールドの修復、データ精度を 加味したパラメータ推計など、多くの問題があり、実用的な解決方法を 探索しています。