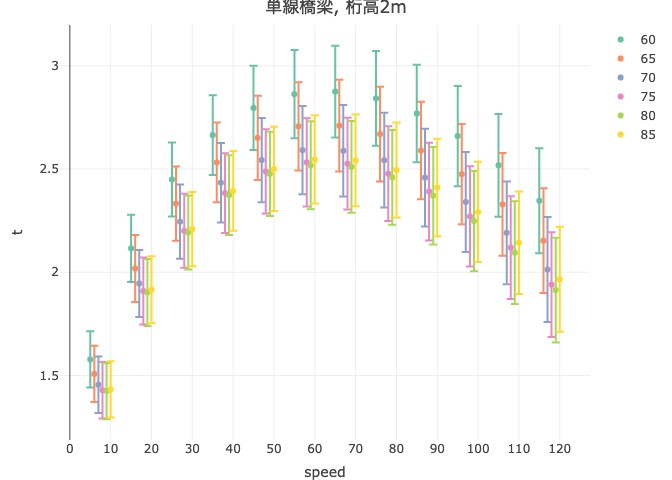
列車の時速とリスク指標（大きいほどよい）の図の一例

リスク評価における積分計算はしばしば困難であり、近似計算のため にマルコフ連鎖モンテカルロ法や逐次モンテカルロ法など様々なモン テカルロ法が用いられます。鉄道総合技術研究所との共同研究では、 強風が列車に与える影響を確率モデルで評価しました。現在、効率的 な積分計算手法の開発に取り組んでいます。これにより、リスクの評価 や不確実性解析をより正確に行い、安全な鉄道システムの構築に貢献 します。

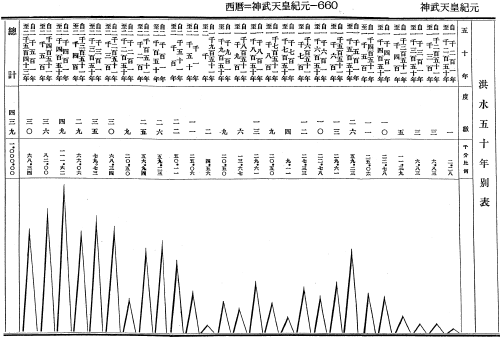50年毎の洪水数の統計（6 世紀から19世紀）

災害は稀に見る豪雨や想定外の大地震によって引き起こされます。このようなリスクを管理する理論として、稀に起こる極端な事象を研究する極値理論があります。極値理論は通常の統計学とは異なる点もあり、マイナーな存在とも思われていましたが、近年その重要性が認識され、研究が盛んになってきています。本プロジェクトは研究集会「極値理論の工学への応用」の開催、本邦初の専門書である「極値統計学（近代科学社）」の出版等を通じてこの分野の発展に寄与しています。

講演する Alexander J. McNeil 教授
（国際シンポジウム「Dependence and Copulas 2015」にて）

金融や保険などの分野で観測される多変量データには、多変量正規分布のようなシンプルな変数間の依存構造を持つ確率モデルではうまく説明できないものが存在します。このようなデータをモデル化するため、近年、「コピュラ（接合関数）」とよばれる多様な依存構造を表現するための確率モデルが着目されています。本プロジェクトグループでは、コピュラにまつわる研究活動を推進しており、Bernsteinコピュラの統計推測理論の発展、周期的な密度関数を持つコピュラの提案、国際シンポジウムの開催などの実績があります。今後も積極的に活動を進めていきます。