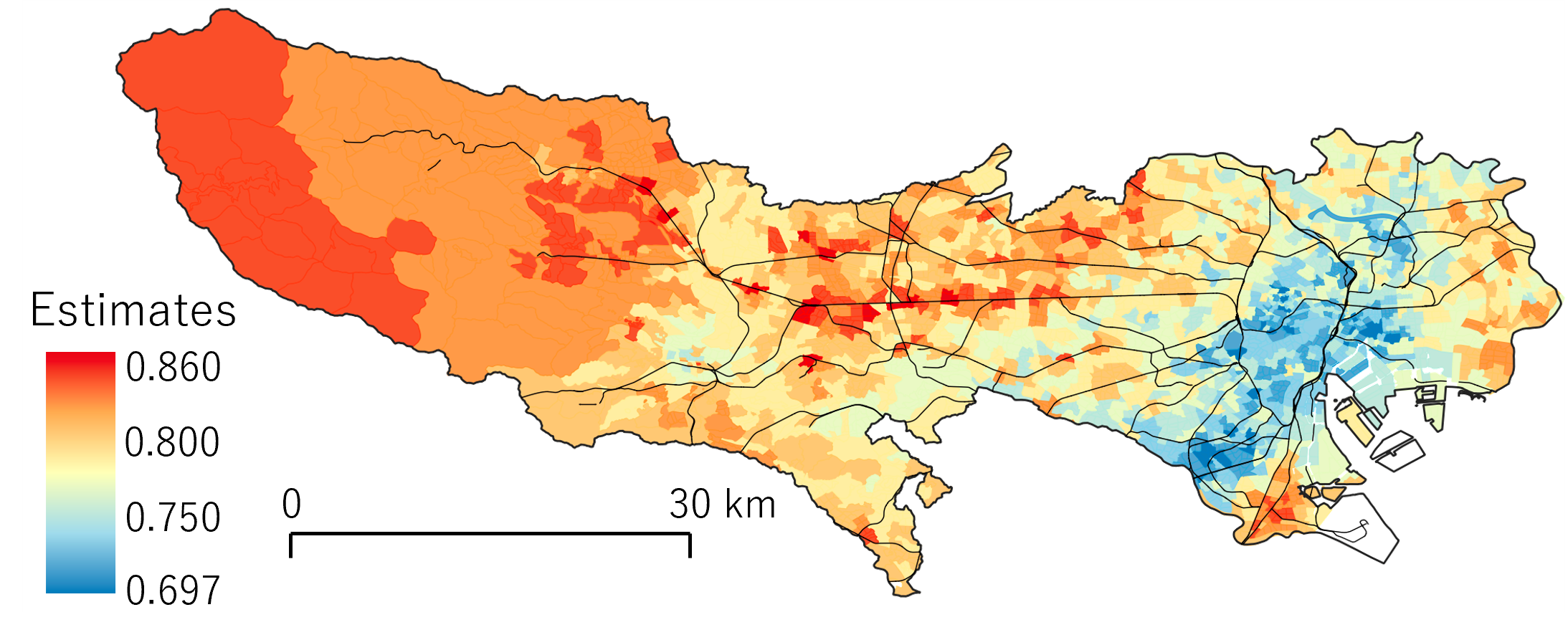Estimated map pattern of the repetitive tendency in bicycle theft

We are developing spatio-temporal statistical models to analyze geographic phenomena and their changes over time. For example, we developed fast spatially varying parameter models estimating latent map patterns underlying, for example, crime occurrence and environmental pollution. The figure on the right shows the estimated map pattern of repetitive tendency in bicycle theft in Tokyo. The result suggests that bicycle theft tends to be repeated in suburban areas especially along certain train lines. Developed methods have been implemented in a package for the free statistical software R. We have also published a book to contribute to the development of related fields.

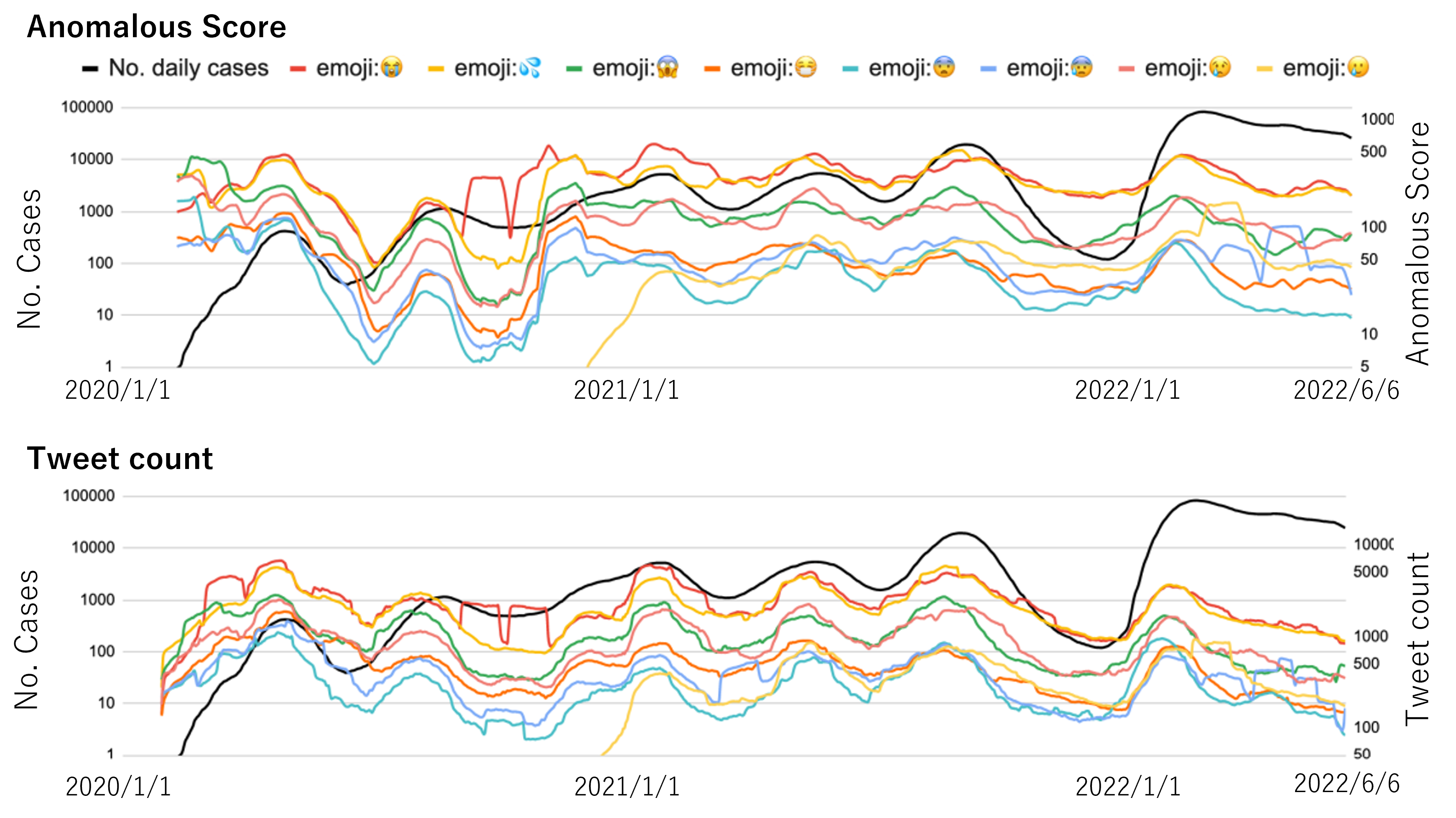Number of COVID-19 cases (black line) and change in tweets per emoji over time (top: Anomalous score, bottom: number of tweets)

It is an important issue to clarify factors contributing to the spread of coronavirus disease 2019 (COVID-19) in preparing for the current and future pandemics. Since 2020, we launched “COVID-19 Response Project” and have been conducted studies on monitoring, forecasting, and hotspot detection of COVID-19 infection at the national, prefectural, and municipal levels. For example, we performed the prediction of the number of positive cases considering the temporal pattern of “emoji” in tweets (see the figure on the right). Besides, we had hold public symposiums to share research outcomes and exchange ideas.

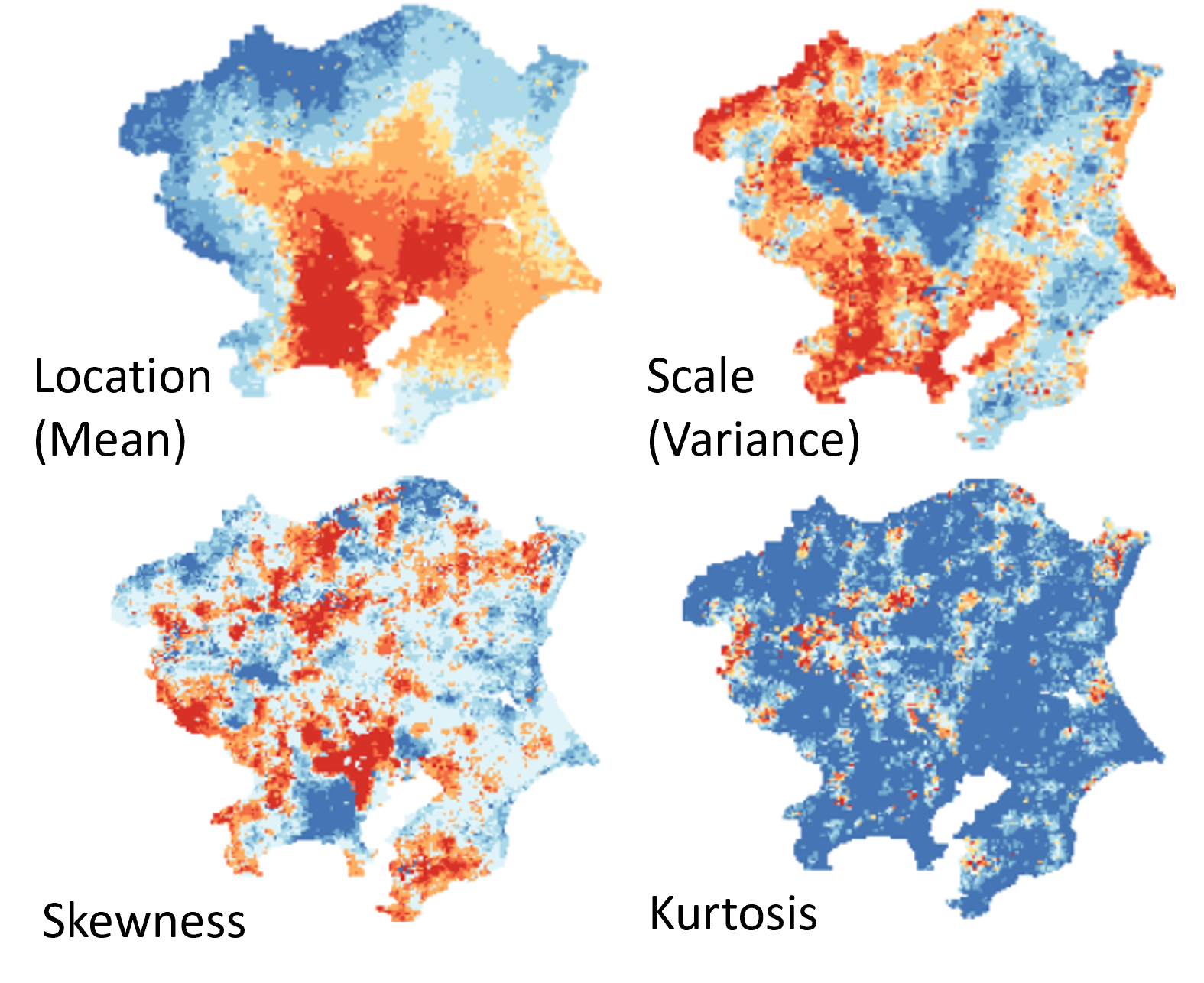Parameter estimates characterizing surface temperature in the Kanto region (August 2013)

Adaptation to climate change is an urgent task. It is especially true in Japan expecting higher flooding and heatwave risks as well as increase of aging population, Given that, we have been engaged in joint research with the Urban Intelligence Project of the Research Center for Statistical Machine Learning on disaster risk impact assessment. For example, we have developed a model to flexibly capture extreme events such as severe heatwaves by combining a spatial process and the Tukey g-and-h random process, which flexibly describes skewness and kurtosis, that are important when dealing with extreme phenomena (see figure on the right).