● Extreme value theory and its application to disaster and other risk management
● Statistical theory of copulas
● Statistical analysis of risk measures for time series data
with complex observation structures
● Statistical inference using semiparametric models
● Promoting exchange in risk management research by, e.g., holding workshops
■ Risk calculation for Strong Winds
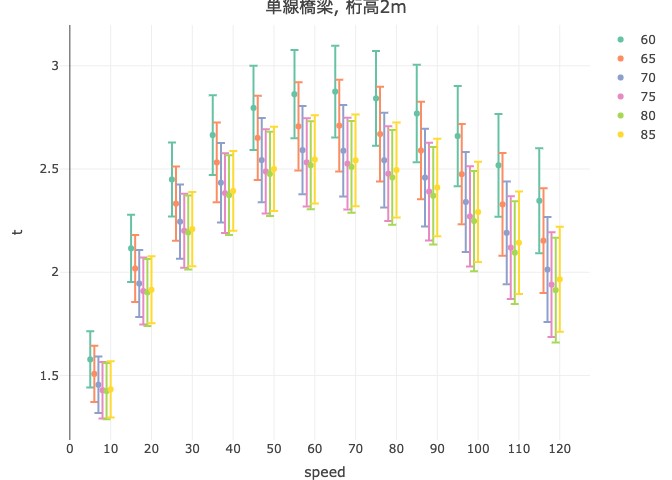An example figure illustrating the train speed anda risk indicator (higher values are better)
Risk assessment often presents challenges in the computation of integrals, leading to the use of various Monte Carlo methods such as Markov Chain Monte Carlo and sequential Monte Carlo for approximate calculations. In collaboration with the Railway Technical Research Institute, we have evaluated the impact of strong winds on trains using probabilistic models. Currently, we are dedicated to developing efficient methods for integral calculations. This will enable more accurate risk assessment and uncertainty analysis, contributing to the establishment of a safe railway system.
■ Extreme value statistics
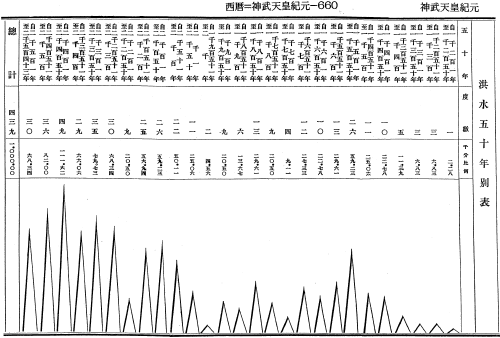Number of floods every 50 years from the 6th to the 19th century
Disasters are caused by rare events such as heavy rains or severe earthquakes. Statistics of extremes is a branch of statistics to study rare events for managing such risks. As it differs from general statistics in some respects, statistics of extremes was considered a minor field until recently. However, its importance has now been widely recognized and extensive research including applications (e.g., engineering and finance) is being conducted. Our project contributes to this field by the annual workshop “Extreme value theory and Applications” since 1994, the first Japanese book on the subject, “Kyokuchi Toukeigaku” (Extreme Value Statistics in English) (2016, Kindaikagakusha) and other activities.
■ Copulas: statistical models with flexible dependence
structures
Prof. Alexander J. McNeil during his lecture
(International Symposium on Dependence and Copulas 2015)
In various disciplines such as finance and insurance, there exist multivariate data which can not be modeled by statistical models with simple dependence structures such as the multivariate normal distribution. For the modelling of such data, statistical models with flexible dependence structures, so-called copulas, have gained popularity of late. Our project group has been working on research activities related to copulas. We have: developed theory of statistical inference for Bernstein copulas, proposed copulas with periodic density functions, and hosted an international symposium, among other efforts. We constantly strive to work on this intriguing research topic.