マッチングサービスや物流の効率化、機械学習など、現代社会のさまざまなシーンで活用されている「組合せ最適化」。扱う要素が増えると計算時間が指数関数的に急増する問題を解決するため、多方面で数学的なアプローチがなされている。経済学でいう「限界効用逓減性」に基づく「劣モジュラ最適化」を拡張することで従来の理論を拡張し、未知の応用領域を切り開こうとする3人の研究者に話を聞いた。
予測・制御科学をドライブする組合せ最適化のフロンティア
私たちの身の周りには、限られた資源の中で「最も良い選択」を見つけ出す必要がある問題が数多く存在する。例えば、物流ルートの最適化、携帯電話などの基地局の配置、機械学習モデルの解釈など、多種多様な課題がこれに該当する。これらの問題を効率的に解くための方法論が、数理最適化の一分野である「組合せ最適化」だ。
統計数理研究所の相馬輔准教授、神戸大学理学研究科の岩政勇仁准教授、北海道大学化学反応創成研究拠点の大城泰平特任准教授の3人は共同で、この組合せ最適化のフロンティアをさらに広げるべく、「部分空間を変数とする劣モジュラ最適化の構築」というテーマに取り組んでいる。科学技術振興機構(JST)の2024年度戦略的創造研究推進事業(さきがけ)のうち、「新たな社会・産業の基盤となる予測・制御の科学」を戦略目標とするプロジェクトの一つとして採択されたものだ。まだ始まったばかりのプロジェクトでありながら、すでに国際会議で採択されるなどの大きな成果を上げている。



経済学の概念を数学的に抽象化した「劣モジュラ関数」
組合せ最適化は、「離散的な対象の中から最も良いものを効率的に求める方法論」と定義される。ただ、最適な解を見つけるために全ての可能性を試す「全探索」では、問題の規模が少し大きくなるだけで計算に天文学的な時間がかかってしまう。そのため、より効率的なアルゴリズムの開発が求められている。
この分野で特に重要な役割を果たすのが「劣モジュラ関数」だ。経済学には「限界効用逓減性」という概念がある。既に多くのものを持っている場合、新しく何かを追加したときの「価値の増加分」が、何も持っていない場合よりも小さくなるという直感的な性質を意味する。
劣モジュラ関数は、この限界効用逓減性を数学的に抽象化したもので、要素を追加するごとに、その追加による効果が減少する性質(減少性)を持つ(図1)。劣モジュラ関数の最大値または最小値を求めることで、大量のデータから重要なデータを選び出すのが「劣モジュラ最適化」だ。

「劣モジュラ最適化は、グラフやネットワークなどの離散的な対象を扱うさまざまな問題を統一的に表現できる幅広いモデリング能力と、効率的なアルゴリズムとを兼ね備えた非常に強力な枠組みです」と相馬は説明する。オペレーションズリサーチ(OR)や数理工学、機械学習といった幅広い分野で役立つことが知られている。
古典的な劣モジュラ最適化の代表例としては、1930年代に研究された「二部マッチング」と1960年代に盛んになった「ネットワークフロー」が挙げられる。二部マッチングとは、例えば男女のペアリングや病院と研修医のマッチングなど、二つのグループに分かれた対象間の最適な組合せを見つける問題のことだ。これを進化させたのがネットワークフローであり、効率的なアルゴリズムによって組合せ最適化の応用範囲を飛躍的に広げた。例えば、物流、交通、避難経路設計など、ネットワーク上での最大流量や最小コストの経路を見つける問題などに幅広く応用されている。
これらの問題は、劣モジュラ関数の良い性質を活用することで、多項式時間で効率的に解くことが可能となる。
対象を部分空間へ拡張することで抽象的で広範囲な問題を表現
しかし、2000年代以降、従来の劣モジュラ関数の枠組みからはみ出すような、新しいタイプの問題が出現してきた。その代表例が「作用素スケーリング」や「Brascamp-Lieb(ブラスキャンプ-リーブ)多面体」などに関する問題だ。
作用素スケーリングは二部マッチングを拡張したもので、類似はしているものの、従来の「集合関数」の概念では理解しきれない性質を持っている。二部マッチングに作用素スケーリングが対応するように、ネットワークフローに対応するものは何か。3人の研究は、まずそれを明らかにすることから始まった。二部マッチング以上に応用範囲が広いネットワークフローを拡張することができれば、実社会に大きく貢献できる。
相馬はそれ以前から、「ネットワークフローが二部マッチングから進化したように、二部マッチングを拡張した『スケーリング』の手法が、ネットワークフロー的に拡張できるのではないか」と漠然と思っていたという。そこから、学生時代からの知己でいずれも組合せ最適化を専門とする岩政准教授と大城特任准教授に声をかけ、共同研究が始まった。
研究の結果、相馬たちはネットワークフローに対応するのは「クイバー表現に対するスケーリング」であると結論付けた。そして、これを定式化しつつ、行列計算を使えば効率的に解けることを明らかにした。さらに、クイバー表現が作るこの新世界にも劣モジュラ性があり、それを利用すると強多項式時間アルゴリズムによって高速で計算できることも示した(図2)。
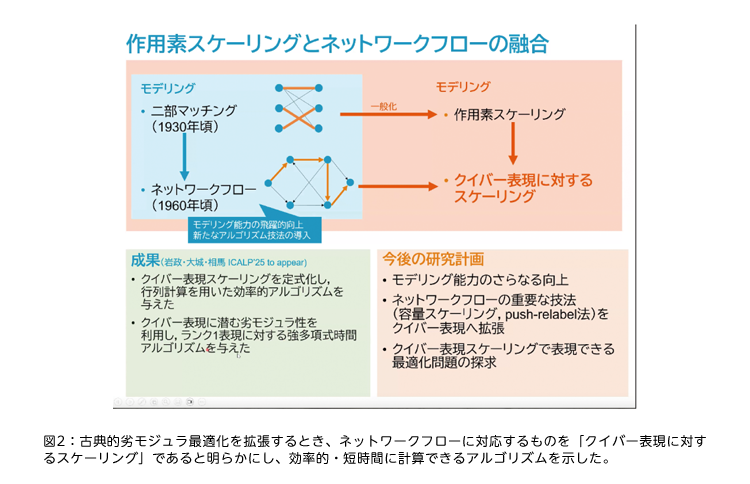
この「新世界における劣モジュラ性」こそが、相馬らが提唱する「部分空間上の劣モジュラ関数」という新しい概念だ。扱う対象を「部分集合」から高次元空間における直線や平面といった「部分空間」へと拡張し、数値を割り当てることで、より抽象的で広範な問題を表現しようとするものだ。この新しい枠組みを構築することが、さきがけプロジェクトの大きな目標の一つとなっている。
代数の世界の「クイバー表現」をスケーリングに援用
3人の論文は、国際会議ICALP 2025に採択されている。だが、成果が出るまでには、試行錯誤の日々もあった。相馬によれば、「クイバー表現」は代数学の分野で研究されてきた概念で、グラフの枝の上に「行列」を乗せたような構造(=有向グラフ)を指す(図3)。純粋数学の道具として、物事を視覚的に理解するための表現方法として使われてきたという。「クイバー」という言葉は、英語で「矢筒」を意味し、日本語では同じ意味の古語である「箙(えびら)」と訳されることもある。

新しい世界でネットワークフローに相当するものを探しているとき、相馬が代数の論文中にクイバーに関する記述を見つけたのがきっかけだった。3人は、「クイバー表現を使うとネットワーク構造のあるスケーリング問題が作れる」というアイデアをもとに、専門外の代数を勉強しながら研究を進めていった。その過程では、数カ月間検討していたものが、ある日「全然ダメだ」と分かることもあった。しかし、古典的なネットワークフローが持つ「流量保存」のような重要な性質が、新しく作った問題の特殊なケースとして再現されることを確認したとき、「これでいける」と確信したという。
大城特任准教授は、「クイバー表現という概念自体が私には目新しいものでした」と振り返る。それが自身の専門とする劣モジュラ関数の性質と結びついていることに「新しいけれど、どこか懐かしい面白さを感じました」と話す。また、岩政准教授は「一人では陥りがちな“閉じこもり”から脱し、多様な視点から議論することで、正しい方向に研究を進めることができました」と、共同研究の意義を述べる。
さまざまな分野への応用と未来社会へのインパクト
クイバー表現スケーリングの発見は、まだ始まったばかりのプロジェクトの「ステップ1」に過ぎない。今後、研究チームはこの新しい枠組みにおいて、古典的なネットワークフローで培われてきたさまざまなアルゴリズム技法を移植し、さらに高速なアルゴリズムを開発することを目指している。また、クイバー表現スケーリングで表現できる新しい最適化問題を探求することも重要なテーマだ。
具体的な応用分野としては、まだ模索段階であるものの、制御理論におけるプラントの最適制御や化学反応系の設計が考えられる。ネットワーク上の化学物質の反応を、行列を用いたクイバー表現でモデル化することで、これまでよりも広い範囲の対象の制御が可能になるのではないかと期待されている。
統計・機械学習分野への応用も視野に入っている。例えば、主成分分析における低次元空間の選択や、共分散行列のロバスト推定(異常値に強い推定)において、部分空間上の劣モジュラ関数の最小値の性質が役立つ可能性があるという。
岩政准教授は「作用素スケーリングと二部マッチングが対応するというのは、比較的新しい発見です。スケーリングという概念を使わずに、古典的なアルゴリズムを自然に拡張したものがクイバー表現に対して作れないかという方向性も探求したい」と語る。数値情報に依存しない「組合せ的アルゴリズム」をクイバー表現に移植することで、計算誤差の影響を受けにくい安定したアルゴリズムの設計が可能になると期待されている。
相馬はさきがけプロジェクトの最終目標として、「部分空間を扱う新しい組合せ最適化の枠組みの構築」「行列計算による実用的・効率的なアルゴリズムの開発」「社会課題解決に欠かせない最適な意思決定の方法論の提供」の3点を掲げている(図4)。

このプロジェクトは、組合せ最適化の古典的な理論を拡張し、新しい数学的構造と計算手法を融合させることで、未知の応用領域を切り拓こうとする大きなチャレンジだ。3人の研究者の密接な連携と、既存の枠組みにとらわれない探求が、最適化の新たな未来の創造につながる。プロジェクトの成果がやがて、社会に大きなインパクトをもたらすだろう。
(広報室)
