世の中が目まぐるしく変化する現代社会。世界中で政治経済が混迷を深める中、EBPMの重要性に対する認識が高まっている。

日本でも政府や自治体は、前例や経験だけに基づく「エピソードベース」では根拠や分析が不十分だとして、変化が生じた要因についての事実関係をデータで収集し、検証する「エビデンスベース」の政策立案へと舵を切ろうとしている。

そうした潮流にあって、エビデンスとなる信頼性の高い資料づくりへのニーズが高まるなか、浮上してきたのが標本調査の分析におけるサンプルサイズの問題だ。

データが全体としては十分に大きくとも、特定の地域（小地域）ではサンプルサイズが十分に大きいとは言えず、安定した推定が難しいケースが発生する。例えば、平均所得や貧困率を推定する際に、市区町村単位ではサンプルサイズが大きいとは言えず安定的な推定ができないことが少なくない（図1）。

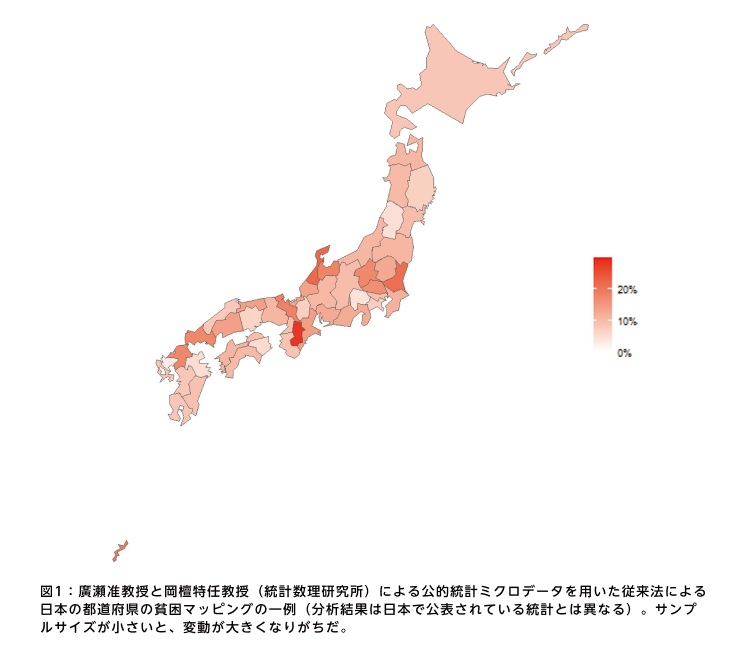
そのような場合に、周辺地域のデータなどを活用して、その小地域の特性値を効率よく推定しようというのが、「小地域推定」と呼ばれる統計手法だ。九州大学マス・フォア・インダストリ研究所の廣瀬雅代准教授は、長年にわたり小地域推定法の理論と応用の研究に取り組んできた（図2）。

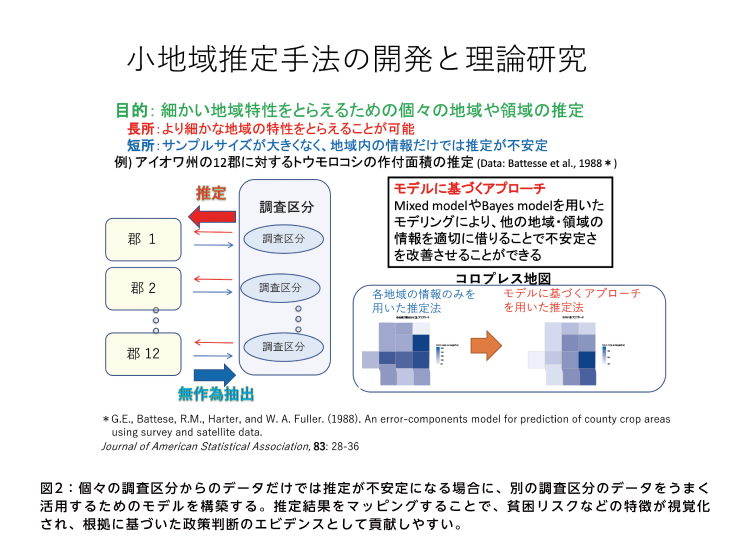
「EBPMの推進は、行政サービスなどの形で国民に適切に還元されることにつながるはず。公的統計ミクロデータなどを使って、EBPMなどにも利用できる信頼性の高い資料を作るには、小地域推定法を統計的に改善する余地があるのではないかと思い、追究しているところです」と廣瀬准教授は話す。

以前、統計数理研究所に所属していた廣瀬准教授は、海外の研究者と共同で、基本的モデルを基にして、複数の有用な数学的性質・統計的な精度を保ちつつ、現実に起こりうる問題をも回避した小地域推定法の新たな推定手法を開発。同じテーマを扱う研究者たちにインパクトを与えた。

だが、廣瀬准教授はこの成果だけで満足したわけではなかった。未解決の問題が残っていたからだ。「基本的なモデルをもっと拡張したかったのですが、数学的に考慮しなければならないことがたくさんあり、少しでも拡張すると解が求まらない状況でした」と廣瀬准教授は振り返る。

そんなとき、統数研のオープンハウスで間野修平教授と出会ったことが、ブレイクスルーの一歩になった。「廣瀬さんと初めて話したのは、たしか2016年頃、統数研のオープンハウスでのことでした」と、間野は記憶している。廣瀬准教授のポスターセッションで、間野が質問したという。

それが交流のきっかけとなり、間野が企画した「統計的開示制御」をテーマとする研究集会に、発表者として廣瀬准教授を招待した。統計的開示制御とは、秘匿が必要な可能性のあるデータおいて、対象に想定される範囲外のデータや異常な変動を特定し、その原因に対策を講じることで開示時の特定リスクを低くするなどの研究トピックだ。

間野は、微分と積分の方法を用いて曲線や曲面などの幾何学的な性質を明らかにする微分幾何学に詳しい。「われわれの考えてきた手法と微分幾何的な方法をつなげると、何か面白いことが言えるのではないかと思い、間野先生に相談したところ、興味を持ってくださったのです」（廣瀬准教授）。

2019年4月に廣瀬准教授が九州大学へ転籍した後も、二人はメールやオンラインでディスカッションを続けた。考察を深めていく過程では、廣瀬准教授が手がけた小地域推定の手法が、統計的開示制御にも応用できることが分かってきた。

統計的開示制御は、公的ミクロデータの二次利用などで問題となる統計法の順守やプライバシー保護に関する研究トピックだ。調査個票には回答者の属性情報が付随していることから、個人が特定されるリスクを回避するために、二次利用の際にはデータ集約などの処置を取る必要がある。

例えば、データが個票で与えられている場合、カテゴリーで分類した分割表を作る。このときクロスしたマスに該当するデータが1つしかない場合、個人が特定されてしまうリスクがある（図3）。もし母集団でも1つしかないと、そのデータの提供者を特定することが可能になる。これを母集団一意と呼ぶ。その期待値をリスク関数としてパラメータ推定を行うのが、統計的開示制御の一つの研究トピックだ。つまりこれにより、作成した分割表にどの程度のリスクがあるかが分かる。

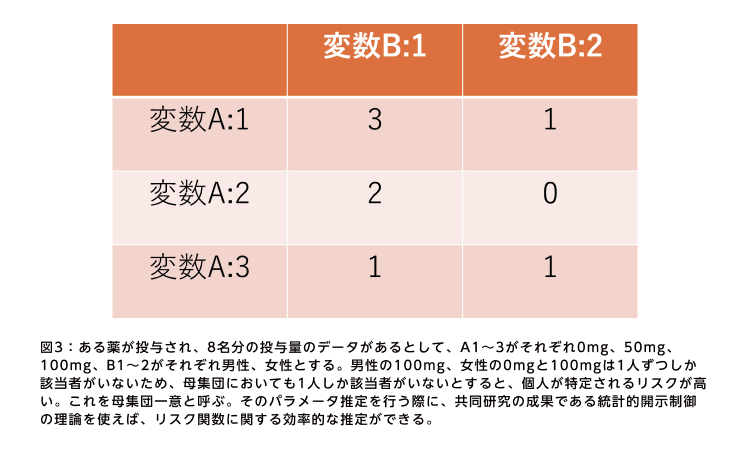
「マスの数字が小さいほどリスクが高いので、カテゴリーを集約して数字を大きくしなければいけませんが、大きくしすぎると特性が見えにくくなる。リスクと特性の抽出はトレードオフの関係にあるわけです。そのバランスをうまく調整するのが、よい推定法です」と間野は説明する。

廣瀬准教授と間野が開発した理論は、分割表の有用性を保って母集団の特性を明らかにしつつ、リスクを低減することにつながる。二人は研究成果を2023年に論文としてまとめた。

統計的開示制御と並行して進めていた小地域推定モデルの拡張についても、大きな進展があった。二人が着目したのは、小地域推定モデルに対し微分幾何学的に最尤法を用いる方法だ。

最尤法とは、平たく言えばパラメータをもつ確率分布の関数の中から最も確率または確率密度を大きくするパラメータを探す手法だ。しかし、最尤法は、サンプルサイズが小さいと大きなバイアスを生じさせる可能性がある。

「廣瀬さんは、開発した小地域推定手法の関数が山のような曲面を描くことから、より一般的なモデルにおいてもそれを幾何学的に解釈できないかと考えていた。話を聞いて、私もそれは可能だと思い、研究がスタートしました」と間野は説明する。

最も確率を大きくするパラメータを選ぶには、微分した解が0になる方程式を解く必要がある。間野と廣瀬准教授は、以下の式を導き出した。

2〈grad l̃,gradf〉+Δf =0

「Δf（デルタ・エフ）」のfは推定したいパラメータの関数、Δはその関数の曲がり具合を意味する。「gradf（グラディエント・エフ）」はfの勾配、「l̃（エル・チルダ）」が「拡張」だ。「つまりこれは、fを与えるとl̃の拡張の仕方が分かる確認式であり、l̃についての準線形1階偏微分方程式です」（間野）（図4、5）。

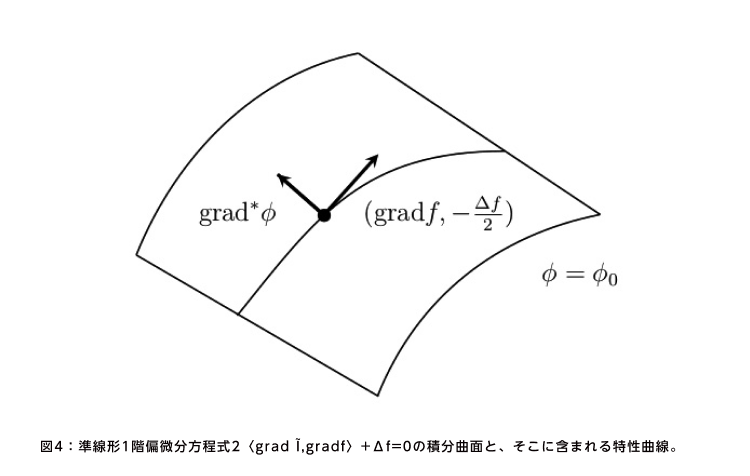
「偏微分」はたくさんの変数について微分を取ることを示し、一般的には方程式を解くのが難しい場合が多い。ところが、準線形1階偏微分方程式は特殊で、完璧に解き方が明らかになっているという。つまり、幾何学的で単純な準線形1階偏微分方程式に落とし込んだことで、懸案であった小地域推定モデルへの手法の拡張が可能になったのである。

「この条件式を満たす例は、さまざまな可能性を秘めています。小地域推定モデルへの拡張もそうですし、前述の統計的開示制御もそう。さらに、Δfを計算すると、f(μ)のよい推定もできるのです」（廣瀬准教授）。f(μ)の推定とは、パラメータμの関数f(μ)の値を、母集団から抽出した標本データに基づいて推定する方法だ。

μの推定法は1990年代から知られていたが、非線形の関数ではバイアスが生じてしまい、使えなかった。廣瀬准教授と間野が開発した新しい推定法は、非線形関数も含めて推定できる手法をより一般的なモデルへ拡張した形になっている。

「準線形1階偏微分方程式の幾何学的解法は、19世紀にフランスの数学者ガスパール・モンジュが開発した、古くからある手法です。偏微分方程式を解くのに微分幾何を使うアイデアは、もう少し新しくて20世紀の初め頃、やはりフランスの数学者であるジャック・アダマールによって提唱されました」と間野は話す。

そうした古典的な手法を現代のニーズに合わせて“引き出し”から取り出し、組み合わせることで新たなイノベーションを生み出す。そこに数学や統計学の面白さとポテンシャルがある。

「今回の論文を書くにあたって、モンジュやアダマール、マルツェル・リースなどのフランス語の古い論文を改めて読み込んでみたら、証明の仕方に時代を感じたりして、わくわくしました。若いときに学んだこれらの数学の知見を掘り起こしてみると再発見があり、改めて役立ったと思います」。研究者らしい間野の感想だ。

アメリカでは国勢調査局（U.S. Census Bureau）が貧困率の分析に小地域推定を用いるなど、この分野の研究と応用が進んでいる。「日本でも、貧困率など地域差をていねいに見ていくべきテーマは多くあります。日本はまだ、小地域推定の手法がすぐに採用される状況ではありませんが、EBPMの進化に向けて理論を構築し、足場を固めていきたいと思っています」と廣瀬准教授は前を向く。

間野もまた、「これまで一人で研究を進めることが多かったですが、統数研は大学共同利用機関法人ですから、廣瀬さんと出会い、今回のような形で有意義な貢献ができたことは嬉しく思います」と話す。

偶然出会った異分野の研究者同士が、それぞれの問題意識と蓄積した知見を持ち寄ることによって、思いがけない発見が生まれる。間野と廣瀬准教授の共同研究の過程を聞くうちに、“セレンディピティ”という言葉が思い浮かんだ。