かつては「無限の宇宙」という言葉をよく耳にした。しかし現在の科学では、少なくとも観測可能な宇宙には限りがあることが分かってきた。

地球は太陽系の一部であり、太陽系は天の川銀河の一部であり、天の川銀河は「局所銀河群」と呼ばれる銀河群の一部だ。銀河群はおよそ50個以下の銀河の集まりで、それより大きく数千個以下の集まりは「銀河団」と呼ばれる。銀河群や銀河団は、さらに大きな「超銀河団」の一部を成している。

こうした階層的な構造の最も大きなスケールが「宇宙の大規模構造」だ。「少なくとも観測された範囲では、それ以上の大きな構造は見られません」と、高エネルギー加速器研究機構（KEK）素粒子原子核研究所理論センターの松原隆彦教授は話す。

松原教授の研究テーマは宇宙論、つまり宇宙の全体構造を理論的に解き明かすことだ。宇宙の大規模構造がどのように形成されたかは、その有力な手がかりとなる。アプローチの仕方は多様だが、その中にミンコフスキー汎関数（MF）やトポロジカルデータアナリシス（TDA）の援用がある。

宇宙には星や銀河が紐のように連なった「フィラメント構造」、1枚の紙のような「シート構造」、泡の膜に沿って分布している「泡構造」などが含まれ、全体として非常に複雑なネットワーク状の形をしている。銀河が群れ集まっているこうした形態を計量化する際、部分を取り囲む「閉じた面」の形をトポロジーで考える方法として、ジーナス統計量やそれを一般化した「ミンコフスキー汎関数」、ベッチ数などがある（図1）。

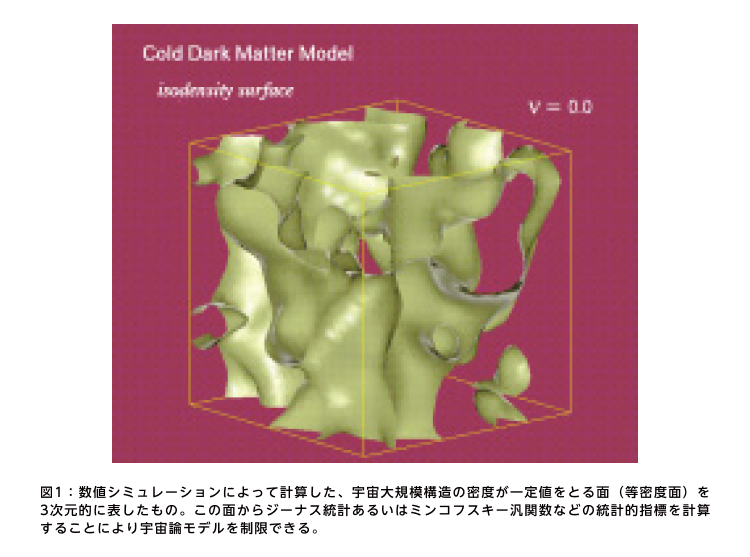
ここでトポロジーは位相幾何学とも呼ばれる数学で、図形を連続的に変形させても穴の数や、つながった部分などが変わらない性質を扱う。例えば、真ん中に穴の空いたドーナツと、取っ手の部分に穴が空いているコーヒーカップは、トポロジーでは同じ種数を持った同じ種類の形として扱われる。

一方、統計数理研究所の栗木哲教授は、確率過程や確率場（例えば画像信号）の最大値分布を評価するオイラー標数法などを専門としている。ここでも先述のジーナス（オイラー数）やミンコフスキー汎関数が登場する。ミンコフスキー汎関数とは、ある集合の大きさや形を測るための関数であり、オイラー数はトポロジーの基礎的な概念の一つだ。

栗木は以前、滋賀大学の竹村彰通学長との共同研究で、検定統計量を多様体上の確率過程としてとらえ、その最大値分布を計算する方法を確立。イネの品種改良に関する実験において、異なる種を掛け合わせた場合に、致死遺伝子の組合せを発見する方法を提案するなどの成果を上げている。

2018年頃、東大柏キャンパスの研究集会で知り合った栗木と松原教授は、お互いの研究手法が似ていることで意気投合。松原教授の宇宙論研究のテーマに確率場の幾何を利用する共同研究をスタートさせた。東大での研究集会は統数研の池田思朗教授が天文と統計学の交流を目的として開いたもの。「見事に掌上に運らされたようです」と栗木は笑う。

それ以降、2024年度現在も文部科学省の科学研究費補助金「基盤研究B」を得て、「確率場データ解析のための積分・位相幾何的手法と期待オイラー標数法の新展開」のテーマで研究を続けている。

「初めのうちは天文や宇宙の言葉に慣れるために、とにかく松原さんと会って話をしました。宇宙の研究者で自分と同じ手法に興味を持つ人がいたことや、自分の得意分野を宇宙の解明に活かせることが嬉しかった」。栗木は、当時のことを楽しげにそう振り返る。雑談の中で偶然、名門・長野県上田高等学校の同窓生同士だと分かったことも、二人の距離を近づけた。

二人の共同研究のテーマの一つに、宇宙の「初期ゆらぎ」の解明がある。松原教授はその問題について、以下のように説明する。

138億年前に宇宙が始まったとき、そこには限られた種類の素粒子がほぼ均一に満ち溢れていた。37万年ほどたったころには宇宙は完全に一様ではなく、わずかな非一様性があったことが観測でもわかっている。つまり、場所によって物質が偏在していた。

物質量が多い場所には、重力によってどんどん他の物質が集まるようになり、物質量の濃淡が拡大する。これが物質の「密度ゆらぎ」だ。現在の宇宙に見られる大規模構造は、この現象の結果として形成されたと考えられる。

その解明に役立つのが、「宇宙マイクロ波背景放射（CMB）」だ。宇宙ができたばかりのとき、光は飛び回る電子にぶつかって直進できなかったが、やがて電子が原子に取り込まれて障害物がなくなると、まっすぐに進めるようになった。これを「宇宙の晴れ上がり」という。そのころの光はそのまま直進を続け、現在の私たちのまわりにも降り注いでいる。これがCMBで、温度を持つ電波として観測される。

CMBの温度は、光が発せられた場所の密度に由来することから、温度にゆらぎが認められれば、宇宙の物質に密度ゆらぎがあったことが裏付けられる。この宇宙の初期にあった密度ゆらぎを「初期ゆらぎ」と呼ぶ。「初期ゆらぎの詳細な性質を明らかにすることで、初期宇宙で何が起こっていたのかを解明する有力な手がかりが得られるのです」と松原教授は言う。

CMBの温度が一定でないことは、すでに観測されている（図2）。この「宇宙の温度地図」は2次元確率場であり、これを解析することで宇宙全体のさまざまな特徴が分かる。

確率場において、ある関数が一定の値を超えるような点の集合を「エクスカーション集合」と呼ぶ。CMBで言えば、同じ温度を示す位置を地図の等高線のように「等温度線」でつないだ図形がエクスカーション集合にあたる。

「確率場の幾何は、このエクスカーション集合を扱います」と栗木が説明する（図3）。エクスカーション集合を多面体の集まり（複体）とみなし、その頂点の数から辺の数を引き、面の数を足してオイラー数を計算するのだ。

2次元確率場が等方的、すなわち平行移動や回転をしても確率的性質が変わらないとき、積分幾何ではオイラー数など「ミンコフスキー汎関数」の期待値が簡単な関数で示される。この関数を使えば、確率場の分布形がガウス性か、非ガウス性かを判定することができる（図4）。

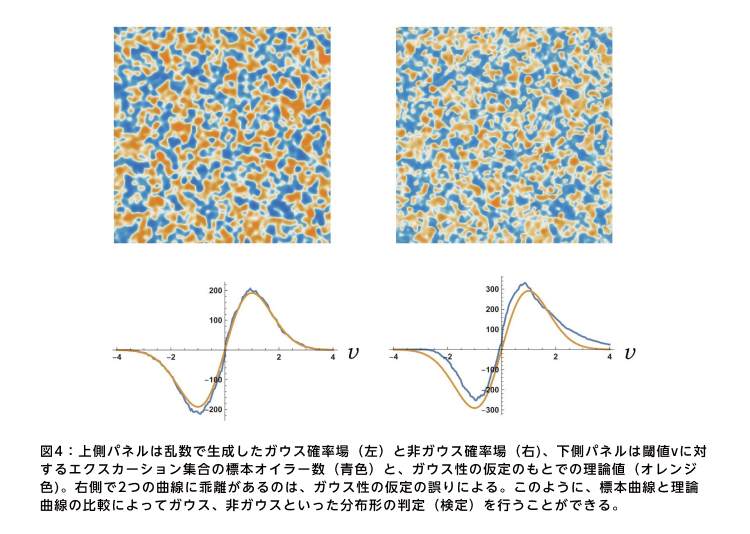
ガウス性とは、データの分布が正規分布（平均値を中心に左右対称な釣り鐘状分布）に従うことを指す。ある閾値に対するエクスカーション集合の標本オイラー数と、ガウス性を仮定したときの理論値を比較し、両者の曲線が一致すればガウス、乖離すれば非ガウスということになる。

初期宇宙の温度ゆらぎを反映したCMBは、等方的ガウス確率場に近いとされており、このプロジェクトでは宇宙モデルの探索のためにオイラー曲線を含むミンコフスキー汎関数の検討を続けている。

宇宙の大規模構造のもとになった初期ゆらぎの情報は、現在の大規模構造のパターンを数値化して定量的に調べることからも得ることができる。それには、銀河の群れ集まり方を数値化するのが有効だ。

具体的には、ある銀河から一定の距離を置いて離れた場所に別の銀河が見つかる確率の高さを示す「相関関数」を使う。周囲に別の銀河がなければ相関関数の値は小さくなり、逆に群れ集まっているところでは大きくなる。銀河が互いに退け合っていれば、値はマイナスだ。

ただし、2つの銀河の間の距離から求める相関関数だけでは、宇宙の大規模構造の全容を捉えることはできない。3つの銀河の距離を数える3点相関関数、4つの銀河の距離を数える4点相関関数などがいくらでも考えられ、それぞれに別の情報を持っている。しかし、高次になるほど計算量は莫大になり、精度の良い観測も難しくなり、コストもかかる。

今回のプロジェクトの大きな成果として、3点相関関数と4点相関関数を用いた漸近展開公式によって、大規模なシミュレーションを代替できるようにしたことが挙げられる（図5）。漸近展開公式とは、ある関数を、別のより単純な関数の和として近似的に表すための公式のことだ。

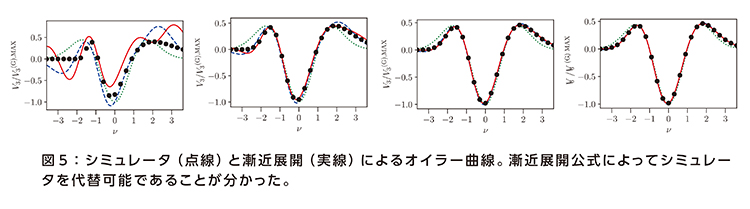
「宇宙の大規模構造を研究するうえで、計算量を減らすことは大きな課題だった。栗木さんと共同研究をして本当によかった」。松原教授はプロジェクトの意義をそう語る。

宇宙論は、今まさに黄金時代を迎えたと言われる。

ユークリッド、ローマン、SPHEREx、ライトバードなどの宇宙望遠鏡、またルービン、スバルHSC/PFSなどの地上望遠鏡といった観測機器・技術が充実し、世界中で大規模な観測プロジェクトが進行。豊富な観測データが得られるようになった。

それに伴い、宇宙ゆらぎや宇宙そのものの起源と進化、ダークマターやダークエネルギーなど未知の要素を含む宇宙の全体像へ迫る研究が、大幅な進歩を遂げているのだ。

そうした中、2024年3月にKEKのつくばキャンパスで、“Statistical Analysis of Random Fields in Cosmology”（宇宙論における確率場の統計解析）と題し、宇宙ゆらぎの統計解析における新しい手法を探求する国際研究集会が開催された。

通称KEK-Cosmoと呼ばれるこの研究会は毎年実施されており、今回は「宇宙論の統計解析」がメインテーマ。世界中から参集した宇宙論の研究者と統計数理の研究者を前に、栗木も招待講演を行った。参加者は約50名に上り、関心の高さが伺われた。

宇宙物理学の世界は対象が明確で2次元、3次元といった具体的な問題に具体的な解を与えることが重視される。一方で数理統計の世界で求められるのは、より一般化した「N次元」での理論だ。

「カルチャーは異なれど、だからこそ互いに刺激を受け、新しいアイデアが生まれる」。7年にわたり共同研究を続けてきた松原教授と栗木は、そう口を揃える。

統計数理の力で、宇宙の解明が大きく前進することが期待されている。