ビジネスや政策決定など社会のさまざまな場面で、データに基づく判断が求められている。データ解析を行う上で最も重要なのは、対象とする数値データに当てはまりがよく、予測精度の高い統計モデルを使用することだ。統計数理研究所の二宮嘉行教授は、「あらゆるデータ解析において、どの統計モデルを用いるかを決める『モデル選択』のプロセスは不可欠です」と説明する。

モデル選択には常に、ある問題が付きまとう。モデルのパラメータ数を増やせば、データとの当てはまり（尤度＝適合度）をいくらでもよくすることができる。しかし、そうして複雑になりすぎたモデルは、別のデータに対してはうまく機能しなくなってしまう。いわゆる「過適合」の問題だ。そうかといって、シンプルすぎるモデルでは、データの重要な特徴を捉えることができず、予測の精度が落ちてしまう。

データとの適合度を最適化し、予測精度を担保するには、モデルの複雑さをどこまで許容できるのか。その追究は、統計学の永遠の課題ともいえる。

1970年代の前半、そこにきら星のごとく登場したのが、統数研の元所長である赤池弘次氏が開発した「赤池情報量規準（AIC）」だ。AICは「データとの適合度」と「モデルの複雑さ」のバランスを図るための指標。モデルの尤度を数値化するとともに、パラメータ数に罰則を与えて計算することで、過度に複雑になったモデルが選ばれることを防ぐ。AICの値が低いモデルは、「データに適合していながら、複雑ではないよいモデル」ということになる。

AICには大きく二つの役割がある。一つは、最適な解析結果を得るために利用する変数を、データに基づいて選択することだ。「具体的には」と二宮は例を挙げる。計量経済で、因果推論を用いて政策の介入効果を分析する際、その効果に影響を与える因子として、貧富や地域などさまざまな変数が考えられる。情報量規準を用いれば、「効果を適切に測るにはどの変数をモデルに取り込めばよいか」を決めることができるという。

もう一つの役割は、「統計モデルには含まれていないパラメータの最適値」を決定することだ。データ解析では、そのパラメータ値を適切に定めないと妥当な結果が得られない状況がしばしば現れる。推定と同時にモデル選択を行うLASSOなどのスパース推定の手法にも、「正則化パラメータ」が含まれている。情報量規準を用いれば、その適切な値を与えることができる。

「逆に言うと、AICなどの情報量規準がなければ、われわれは最適な統計モデルや統計手法がどれか分からず、正確な解析結果が得られないということ。情報量規準とはそのくらい重要な、なくてはならないものなのです」と二宮は話す。

AICはその革新性から発表以来またたく間に普及し、モデル選択の標準的な指標となった。今では計量経済や時空間統計、医療統計など分野を問わず重用されている。ただその半面、現状との乖離を指摘する声もある。「統計学では世界的にも知らない人がいないほど有名な指標になっているがゆえに、すでに完成されたものとして改良が進まないきらいがあります」と二宮は話す。

近年は統計学そのものの様相が、AICの開発された時代とは変わってきた。ICTの進歩によってデータは大規模で多様になり、統計モデルや推定法も急速に発展、複雑化している。このため、情報量規準が旧態のまま利用されることで不都合が生じ始めているのだ。

「現代の統計学に、AICをはじめとする既存の情報量規準をそのまま適用すると、大きくミスリードされる、つまり妥当なモデル選択が行われない状況が一部には生じています」。二宮はそう話し、時系列データの変化点解析の例を挙げた（図1）。

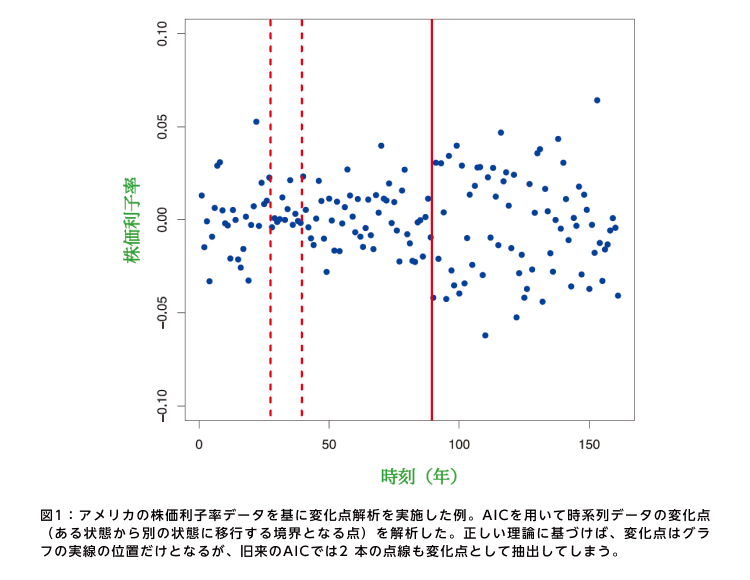
変化点とは、データの発生構造が急激に変わる地点を指す。変化点の有無や位置を明らかにするのが変化点解析だ。「図1の例では、変化点は正しい理論に基づけば実線の部分だけとなりますが、古典的なAICを使うと、過適合により点線の部分までも変化点であるという結果が出てしまうのです」と二宮は説明する。

AICの計算式は、適合度を表す第1項と罰則を表す第2項からなる。「ミスリードが起こる理由は、罰則項の大きさを導く既存の数理が、現代的な統計手法に援用できていないケースが増えているからです」と二宮は言う。

例えば、経済統計分析における因果推論（傾向スコア解折）や機械学習における特異モデル解析では、罰則項を通常より遥かに大きな値としなければならない。一方で、時空間統計分析に欠かせない高次元データ解析では、罰則項は通常より遥かに小さな値としなければならないことが判明している。

「機械学習や人工知能によるデータ解析に頼る時代が到来しつつあります。そこに、数理的な妥当性のない情報量規準を安易に用いることで、不適切な解析結果が世の中に供給され、大きな社会問題につながりかねないリスクがあります」と二宮は危惧する。

こうした現状を何とかしようと、二宮が広島大学の栁原宏和教授、九州大学の川野秀一教授、統数研の川崎能典副所長とともに立ち上げたのが、AICを見直し、現代統計学にフィットするものに進化させるプロジェクトだ。

今回のプロジェクトは、因果推論や高次元データ解析、機械学習における特異モデル解析の拡張や融合に加え、スパースモデリングなど、統計的モデル選択に大きな改良が見込まれる問題のみを対象として、数理的に保証された情報量規準を与えることを目指すものだ。二宮は「プロジェクトの着地点は、意義の大きい問題をすべて取り上げて開発し、新たなAICを普及させるにあたっての主導権を握ることです」と話す。

AICの導出は、標本サイズnを無限大にしたときどのような値に近づいていくかという「漸近理論」に基づいている。「標本サイズだけを大きくする漸近理論を用いていたことが旧来のAICの特徴で、当時は変数の次元が小さかったので、うまく機能していたわけです」。時空間データなど高次元データ解析を専門とする栁原教授は、そう説明する。しかし、大量のデータを取得できるようになり、コンピュータの計算能力も飛躍的に向上した今では、「変数の次元が小さい」という前提自体が崩れている。旧来のAICをそのまま使うことには無理があるのだ。

だが興味深いことに、現代統計学にふさわしく拡張または融合することを考えるとき、AICはベイズ情報量規準（BIC）など他の規準に比べて、よりよい性質を持つことが分かってきたという。栁原教授は次のように説明する。

これまで、AICの弱点は「一致性を持たない」ことだと捉えられていた。「一致性」とは、標本サイズを増やすほど、データの持つ正しい構造を選ぶことができる性質だ。これに対してBICは、一致性を持つ。

しかし、この特性は低次元データに限られたもので、高次元データになると状況が逆転する。「標本サイズと変数の次元を同時に増やす漸近理論で一致性を再評価したところ、AICが一致性を持ち、BICは一致性を持たないという逆転現象が起こることが分かりました。BICは罰則が強すぎて、より変数の少ないモデルを選んでしまうのです」と栁原教授は解説する（図2）。

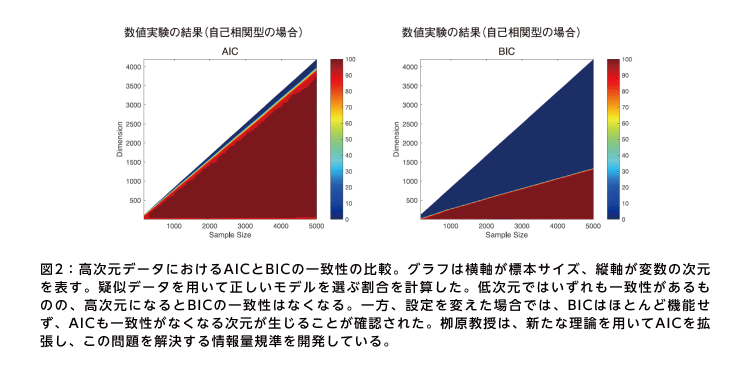
こうした特性は、統計学者の間でもまだほとんど知られていないという。「外国人研究者に話しても一様に驚かれるので、海外も国内と同じ状況なのでしょう」と二宮は言う。いち早くAICの可能性に注目した栁原教授と二宮は、高次元データ解析に即してAICを拡張する研究で成果を上げている。

一方、川野教授の専門はスパースモデリングだ。標本サイズに比して統計モデルに含まれるパラメータ数が多い「高次元小標本」の状況に対し、スパース推定を援用した多変量解析手法の開発研究を行っている。また、統計モデルの事前情報を組み込んだベイジアンモデリング、パラメータの推定値を数値的に求めるための計算アルゴリズムについても広く研究を進めている。

スパースモデリングは、ある結果がなぜ得られたのか、たくさんの要因の中から数少ない本質的に重要な要因を選び出す技術だ。「スパースモデルのモデル選択にも情報量規準を使いますが、古典的な理論ではいい結果が出ません。どうするかと考えていたときに、二宮先生から新しい理論を提案され、共同研究を開始しました」と川野教授は話す。

データから抽出したい情報に応じて統計モデルを設計する際には、罰則項も変える必要があり、そのつど新たな理論を応用し、フィットする情報量規準を使ってモデリングしているという。二宮との共同研究の成果は、2016年にsAIC、2023年にはsmoothing varying regularization（SVaRu）として、Rのパッケージになっている。SVaRuはスパースモデリングの代表的なアルゴリズムであるLASSOを拡張したもので、今はそれ以外についても研究を進めているところだ。

すでに二宮と栁原教授、二宮と川野教授、そして栁原教授と川野教授のペアによる共同研究の成果は、それぞれ論文になっている。各人の専門分野である因果推論、高次元データ解析、スパースモデリングは部分的にオーバーラップしており、その交点に位置するのがAICというわけだ。二宮は今回のプロジェクトについて、「これまで個別にやってきたことを一般的な枠組みとして展開するいいタイミングだと思っています」と期待する。

プロジェクトはまだ始まって1年目であり、今は新たな情報量規準の必要性の認知に向けた種まきをしている段階だ。昨年は統数研の共同利用の重点型研究を企画し、公募で共同研究課題を募った。3月8日に初めて本格的に実施した研究集会には、海外の研究者も参加。翌9日の統計学会春季集会でも、招へいした外国人研究者と栁原教授が同様のテーマで講演を行った。

こうした精力的な啓蒙活動により、さまざまな分野の研究者とのディスカッションを通じて、可能性のあるテーマが続々と見つかりつつある。川野教授は「統計ユーザーの研究者の中には、旧来のAICを微調整して使いながらも、満足していない人が少なくない。そういったニーズを掘り起こしていきます」と話す。

栁原教授は「究極的には、誰もがどんなケースでも修正などをする必要がなく、何も意識せずに気軽に使えるユーザーフレンドリーなAICを世に出したい。このプロジェクトをその第一歩と捉えています」と先を見据える。川野教授も「さらにその先は、いずれ登場するであろうディープラーニングを超える手法にもフィットする、次世代AICの理論の礎を築きたい」と言葉をつなぐ。

AICの“お膝元”である統数研には知見も豊富に蓄積されており、新たなAICを生み出す土壌としては申し分ない。「将来的にはニューラルネットワークモデルを含む特異モデルの正則化にも利用できるAICなど、人工知能モデルや深層学習モデルにも寄与するものにしたい」。二宮はプロジェクトチームを代表して、力強く抱負を語った。