電子スピンと呼ばれる電子の属性がランダムな向きのまま固まった「スピングラス」。その内部では、一つひとつの電子スピンが互いに影響を与え合い、多様な固まりとして共存している。こうした複雑系の相互作用を記述するスピングラス理論は、さまざまな分野の現象に応用できることが知られている。機械学習や生物進化の仕組みを電子スピンの相互作用になぞらえ、画期的な考察を進めるプロジェクトを取材した。
向きがバラバラのまま固まった電子スピン
統計物理学に「スピングラス理論」と呼ばれる理論がある。スピンとは、電子のもつ「磁石のもとになる運動量」のことだ。イメージとしては電子が自転している様子を思い浮かべれば良い。自転の向きに応じてスピンは方向性を持ち、その方向性がN極とS極となる。例えば、磁石が強力な磁力を持つのは、電子スピン一つひとつがそれぞれ同じ方向を向き、N極とS極が揃うからだ。複数のスピンが協調的に働くことで、秩序だった強い磁性が現れる。
これに対し、スピングラスとは「電子スピンの向きが一定方向ではなくランダムな方向を向いたまま固まった磁性体」を指す。その構造が、液体が非均衡な状態のまま固まったガラスの構造に似ていることから、「スピングラス」と名付けられた。スピングラスではスピンの向きがまちまちなので、強い磁性は現れない(図1)。
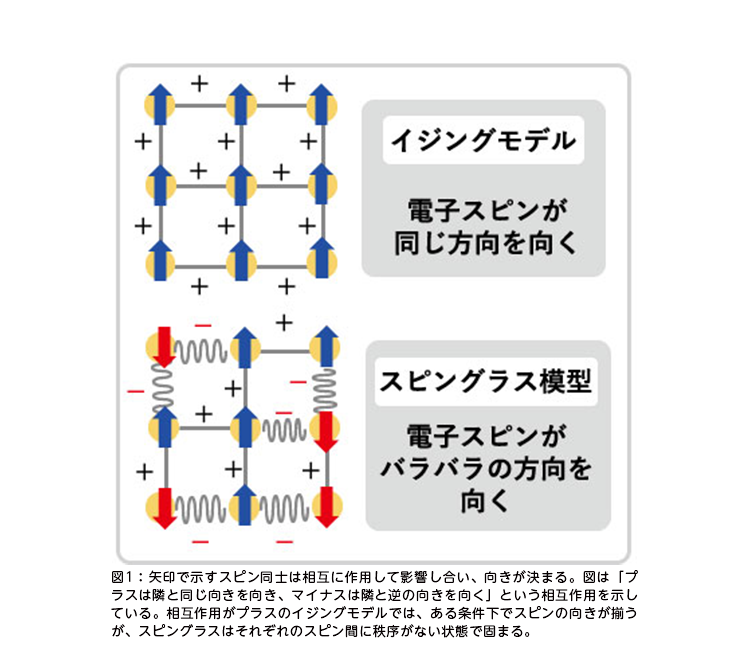
スピングラスのランダムな状態は、スピン間の相互作用や温度変化など些細な条件によって簡単に変化する。ある条件下では、微視的にはスピングラス内に異なる固まり方が多様に共存している。こうした複雑系の振る舞いを記述するための理論が「スピングラス理論」だ。2021年にノーベル物理学賞を受賞した物理学者Giorgio Parisi氏の研究も、スピングラス理論を扱った内容だった。
スパース推定による圧縮センシングへの応用
統計数理研究所数理・推論研究系の坂田綾香准教授は、京都大学大学院情報科学研究科の小渕智之准教授とともに、スピングラス理論を機械学習に応用する研究を続けてきた。二人とも統計物理学の研究室出身で、大学は違ったが院生時代からの知り合いだ。

「機械学習で解きたい問題をグラフで表現すると、スピン間の相互作用を表す方法と類似することが少なくありません。そこで私たちは、スピングラス理論を機械学習に応用する研究を手がけています」と坂田は説明する。
例えば、医学統計分野では患者のデータから患者の病状の経過を予測したいという需要がある。患者の予後と、年齢や性別といった患者の属性、栄養状態や臨床の測定値からなるデータセットを用いて、一つひとつの要素と予後の関連性(相互作用)を表したグラフは、図1のようなスピングラス模型と類似しているという。
「スピングラス理論は機械学習、なかでもスパース推定の解析やアルゴリズム開発に強みを発揮します」と坂田。小渕准教授も「統計物理の手法には近似法など系統的な計算方法があり、それを使うことによって、問題の数学的な構造を他分野とは違う切り口で深く解析できるのです」と話す。

これまでの共同研究の一つに、「圧縮センシングへのスピングラス理論の応用」がある。スパース推定の一種である圧縮センシングは、少ない観測回数でも正しい結果を復元する手法。一例としてよく用いられるのが、医療用のCTスキャンだ。
医療の現場では、X線が人体に与える影響の軽減や検査時間の短縮のために、観測数を減らしたいというニーズがある。スパース推定による圧縮センシングを利用して、「何回の観測を行えば、対象の画像を完璧に再構成できるか」という問題に答えることができる(図2)。
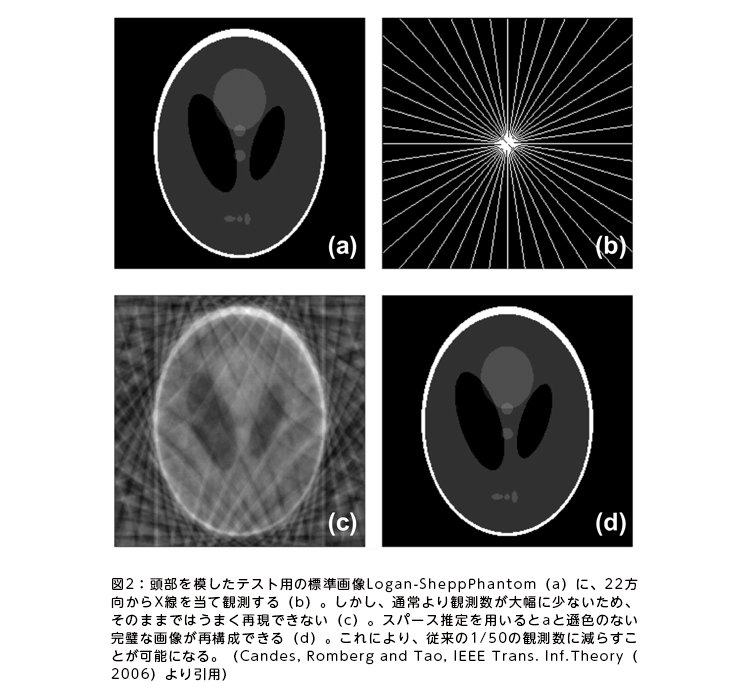
図2の脳のCT画像で言えば、数学的には、写したいものがある(=値がある)領域は限られており、ほとんどの領域の値はゼロとなる。観測結果から脳画像を再構成するときにこの情報を使い、ゼロの位置を推定しながら問題を解けば計算回数を減らすことができ、少ない観測からでも完璧に画像を再構成できる。二人はこの圧縮センシングにスピングラス理論を応用した。
既存研究では「L1正則化」を用いた再構成法が提案されていたが、より少ない観測数で再構成するにはどうすべきかを考察し、統計学において用いられていた「非凸連続正則化」を採用して研究を展開して論文にまとめた(図3、4)。「非凸連続正則化を用いた方法では、より少ない観測回数で再構成できました。機械学習では凸性を持つ正則化のほうが扱いやすいものの、学習精度は落ちてしまいます。そこで、扱いやすさより精度を優先して、凸関数よりも性質が複雑な非凸関数を正則化に採用したのです」(坂田)。
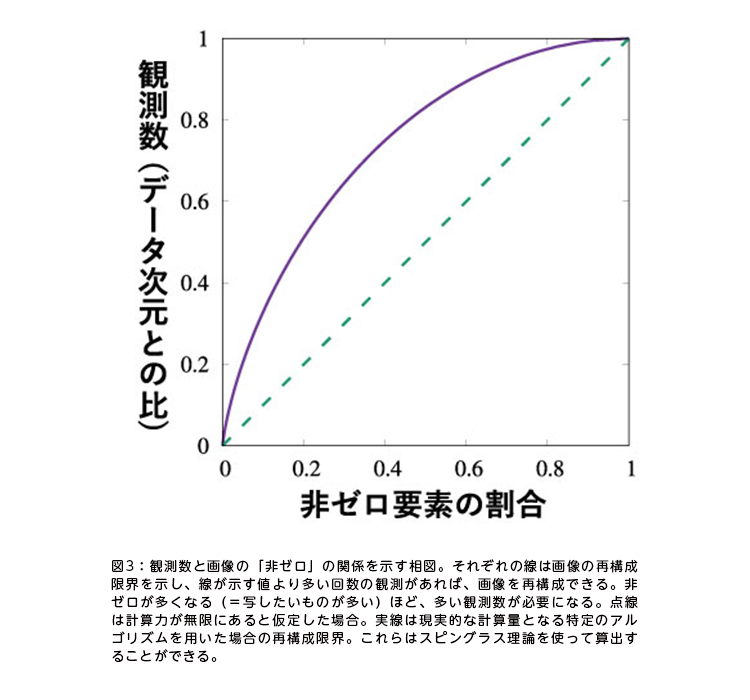
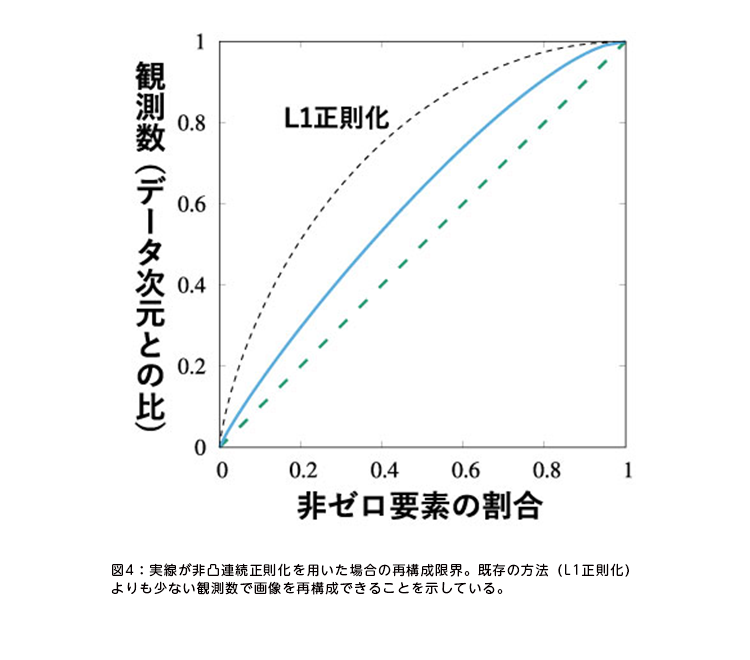
“諦めるべき領域”を明示する「スピングラス転移」の発見
一方、二人はスピングラス理論を活用すれば、機械学習で問題になる「過学習」を防げることも発見した。
じつは、非凸連続正則化による推定の過程で、一つの問題が浮上した。凸関数に対してよい性能を示す既存のアルゴリズムが、非凸では予想した性能が出なかったのだ。なぜうまくいかないのか。二人の想像どおり、その原因は「スピングラス転移」という現象が起こっているからだった(図5)。
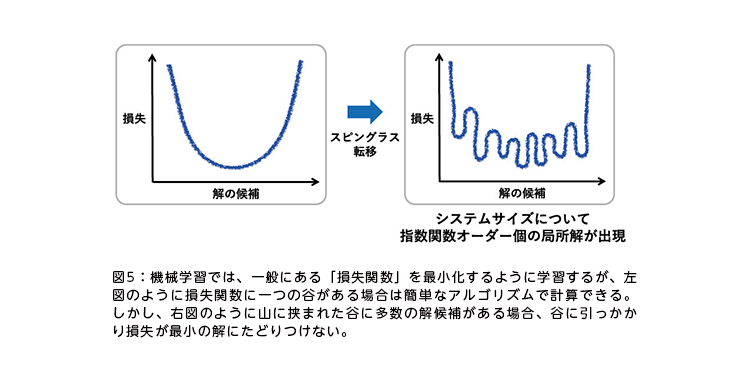
「些細なプロトコルの違いで磁石がスピングラスになってしまうのと同じで、局所的な解がたくさんあるためにこの問題がうまくいかないことを発見しました。これはスピングラス理論以外の方法では見つけにくいと思います」(小渕准教授)。原因が分かれば、対処もできる。アルゴリズムの改善にもスピングラス理論を役立てた。
さらに、L1正則化に対して小渕准教授らが開発した「クロスバリデーション誤差」の計算量を減らす近似方法を非凸関数に対して適用し、実装した。クロスバリデーションは機械学習のモデルの予測性能を測り、過学習を防ぐための手法として知られるが、計算量が大きくなりがちな点が課題だった。非凸関数にこの近似方法を適用すると、計算量が減るだけでなく、スピングラス転移が起きる条件を発見できることがわかった。これにより、適切でないモデル設定を明示する手法を提案した(図6)。
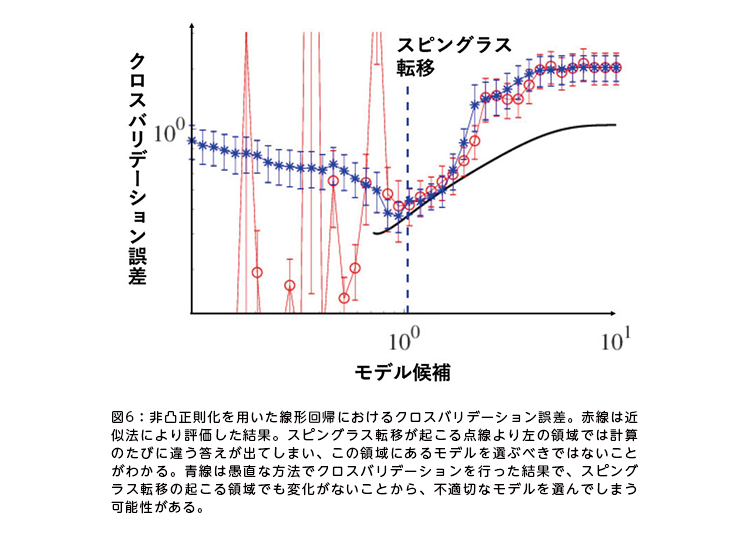
「スピングラスは『諦めの理論』です。スピングラス転移が起こったら、そこから先は計算するたびに違う解になってしまう領域なので、諦めたほうがいいからです」と小渕准教授は話す。
今後は、既存のアルゴリズムがうまく機能しない原因の解明や新たなアルゴリズムの開発に、スピングラス理論を活用していく考えだという。
遺伝子をスピンに見立て進化理論を考察する
スピングラス理論が応用できる範囲は広い。現在、坂田は生物進化理論への応用を研究している。生物の遺伝子を電子のスピンに見立てて考える手法だ。
図1のスピングラスの模型で、スピンを遺伝子と捉え、スピンの相互作用を遺伝子間相互作用に当てはめてみる。すると、一つの遺伝子から作られたタンパク質が他の遺伝子の発現を抑えてタンパク質生成を抑制する(-)、あるいは別の遺伝子のタンパク質生成を促進する(+)などの相互作用を表すと解釈することができる。
「現状の遺伝子間の相互作用は、進化的に選択されてきたものです。一般に、進化は環境への適応度を上げる方向に進むと考えられますが、相互作用の+や-の規則性がどのように生じたかを考察しています」と坂田は説明する。
東京大学大学院の金子邦彦教授(現在はNiels Bohr研究所に所属)との共同研究では、「統計物理のレプリカ対称性が解き明かす表現型進化の拘束と方向性」と題して、新たな理論を開発した。次のような内容だ。
遺伝子の発現量のパターンは、環境変化が起こってもそれほど変わらないことが実験で分かっている。遺伝子発現に関わる要素が変化すれば発現パターンは変わるため、本来ならば発現パターンは膨大であるはずだが、実際にはその中の一部しか発現していない。
遺伝子からどんなタンパク質ができるかは、基本的に遺伝情報に従う。しかし実際のプロセスは分子の反応であり、分子は熱ゆらぎなどの影響を受けて予測不能な動きをすることがある。坂田らは、そうしたノイズがある環境下で進化した結果、発現したパターンが一部のものに限られていることをモデル上で再現した(図7)。
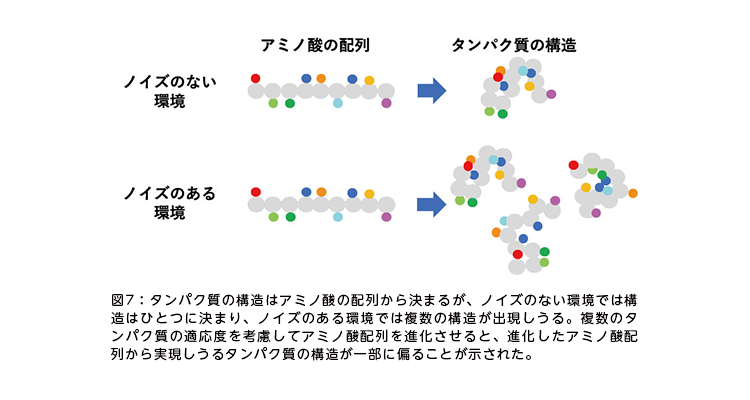
スピングラス模型のスピン変数を何とみなすかによって、遺伝子ネットワークのモデルにもなれば、アミノ酸からなるタンパク質のモデルにもなる。「何にでも応用できる抽象的なモデルだからこそ、遺伝子、タンパク質、細胞といったさまざまな階層に応用できるのではないかと考えています」と坂田は話す。
無限大から導き出す究極のシンプリシティー
坂田がスピングラス理論を物理以外の分野に応用する研究を手掛けるようになったきっかけは、大学2年のとき「『生物の酵素反応』をスピングラスのより単純なモデルである『イジングモデル』で説明できるのではないか」と直感したことだった。
「酵素タンパク質が触媒する化学反応の速度は、酵素が結合する物質の濃度に対するシグモイド曲線となりますが、当時の生化学の講義では『タンパク質間の相互作用によりシグモイド曲線が生じる』という定性的な説明が主でした。同じ頃、物理の講義では『イジングモデルでは電子スピン間の相互作用の結果として磁化が生じ、それはシグモイド曲線で記述される』と数学的に示していました。そこで、生物にもイジングスピンの理論を導入し、スピン変数を生物の構成要素とみなして、要素間の相互作用の結果として生じる現象を数学的に説明してみたいと思ったのです」と坂田は振り返る。
小渕准教授もまた、学生時代にイジングモデルに魅了された一人だった。「物理現象はもちろん、社会現象を説明するなど、いろいろなものに使えるのが面白い。人の噂が75日で伝搬するにはどのくらいの相互作用の強さが必要かをイジングモデルで解いた先輩もいました」と笑う。
小渕准教授は大学院でスピングラス理論研究における日本の第一人者である東京工業大学西森教授の研究室に進み、坂田は東大大学院でスピングラスの進化理論への応用などを研究。その過程で必要性を感じた機械学習の研究にも範囲を広げた。
物理学出身ならではの強みを小渕准教授はこう語る。「高次元極限、熱力学極限といった無限個の変数を処理する解析的なテクニックが統計物理の分野には結構ある。それが他の分野、例えば機械学習や生物統計、進化理論に乗り込んでいくときの武器になると思っています」。
例えば、画像ならピクセル数(n)が無限大の極限を考えるからこそ、逆説的に現れてくるシンプリシティーがあるという。ただし、単純化しすぎると元の現象の本質も失ってしまう。スピングラス理論を進化理論に応用する際も、なるべく元の現象の複雑さを損なわないようにしつつ解析が可能なようにすることがポイントだ。
単純化のジョークでよくあるのが、「牛を球体と仮定する」というもの。もちろん牛の性質の多くは失われるが、これでも例えば「牛とぶつかったときに受ける衝撃を計算する」ことはできる。「単純化して扱える現象と扱えない現象をきちんと切り分け、自分が見たいものが何なのかを考えて現象とモデルを単純化することが重要です」と小渕准教授は話す。
統計物理学の真髄は、微視的な物理法則から巨視的な性質を導き出すこと。スピングラス理論は、さまざまな分野でこれまでとはまったく異なるアプローチによる考察を生み出す可能性に満ちている。
(広報室)
新型コロナウイルス感染拡大防止のため、本インタビューはオンラインで行われました。
