「連続最適化の理論やアルゴリズムの研究者が、応用の研究者と課題を共有し、アイデアを出し合える場をつくりたい。協力してもらえませんか」。統計数理研究所数理・推論研究系数理最適化グループの田中未来准教授は、慶應義塾大学理工学部管理工学科の成島康史准教授、関西大学環境都市工学部都市システム工学科の檀寛成准教授、東京都立大学システムデザイン学部機械システム工学科の豊田充助教に声をかけ、この構想の実現に向けて準備を進めている。

「連続最適化」は「数理最適化」の分野の一つ。数理最適化とは、与えられた条件を満たす候補の中で目的となる指標を最小（または最大）にするものを求めるための数学的方法論だ。高校で学ぶ数学でも「関数f (x )=x ²-2x +3を0≦x ≦5において最小にするx を求めよ」といった数理最適化の問題を目にするし、実社会でも私たちの身近なサービスや産業界のさまざまな分野で応用され、活用されている。

たとえば、出発地から目的地までの複数の経路のうち最も所要時間が短い、最も運賃が安いといったルートを検索できる乗り換え案内や、需要と供給のバランスの中で最も効率よく製品を作る生産計画、複数の工場から複数の店舗まで製品を運ぶのに最も輸送コストが安くなるようにする配送計画などは、数理最適化が活用されている代表例と言える。

機械学習の進化に欠かせない連続最適化の技術

数理最適化は、大きく連続最適化と離散最適化（組合せ最適化とも呼ぶ）に分けられる。「両者の違いは、変数が『連続的に動くかどうか』です」と田中は説明する。

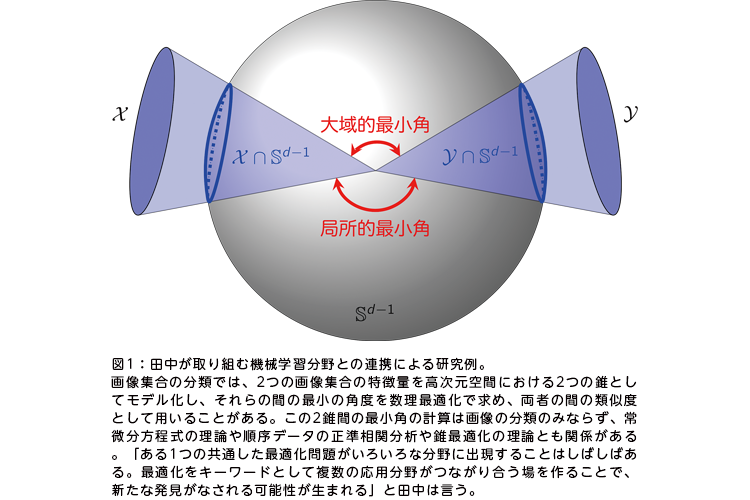
先の例で言えば、交通機関の乗り換えは「Aという乗り物に乗るか、乗らないか。乗らないならBに乗るか、乗らないか」という選択の組み合わせであり、「AとBの中間に乗る」ことはありえない。配送計画でも輸送トラックは1台、2台の単位であり、「0.5台」はない。つまり、これらの問題は、通常は離散最適化の問題として解かれる場合が多い。

一方で、「投資におけるポートフォリオを最適にする」といったケースでは、「収益を最大にする」「リスクを最小にする」といった条件に沿って保有する金融商品の比率を連続的に変更できることから、連続最適化の問題として扱われるのが一般的だ。

数理最適化はこのように応用範囲が非常に幅広いが、最近は連続最適化より離散最適化のほうが隆盛で、研究者も多い傾向にあるという。「統数研には伝統的に連続最適化を専門とする研究者が一定数在籍していますが、国内を見渡すと、連続最適化を選ぶ学生や研究者が相対的に減ってきているように思います」と田中は懸念を示す。

前職では民間企業に所属し、最適化問題の実務課題について相談を受ける立場にいた檀准教授も「持ち込まれる相談の9割以上が離散最適化でした。製造現場などでは離散的、組合せ的な構造を持つ問題ほど表面化しやすいことが一因でしょう。しかし、連続最適化がなくてはならない分野もあるので、絶対に研究の灯を消してはいけないと思っています」と力を込める。

じつは、統計や機械学習を下支えしている技術も連続最適化だという。

「たとえば、線形回帰によって『スポーツドリンクの売り上げを予測したい』というケースを見てみましょう」と成島准教授は例を挙げる。第i 週の売り上げy_i 、平均気温x_{i 1}、平均降雨量x_{i 2} が与えられているとき、モデルy_i =β₀ +β₁ x_{i 1} +β₂ x_{i 2}+ε_i を仮定して、誤差 ε_i の2乗和が最小になるパラメータβ₀, β₁, β₂ を数理最適化で求める。この場合、β₀, β₁, β₂ は連続変数であるから、連続最適化の問題になるわけだ。これは、もっとも単純な例だが、同様の考え方が統計や機械学習の基礎となっている。

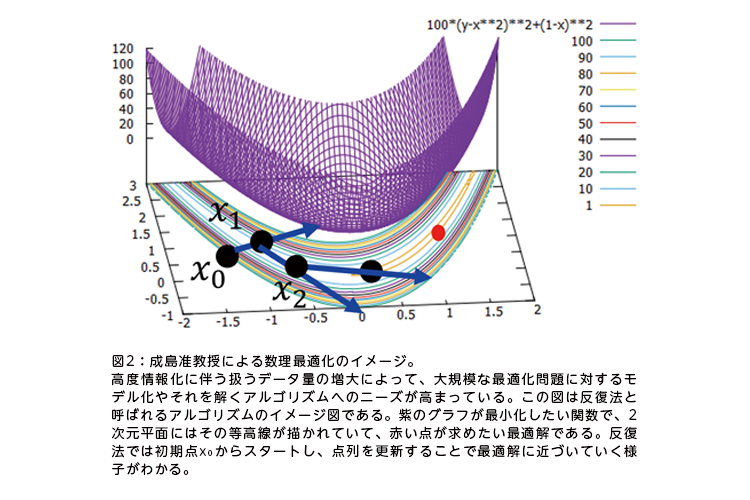
統計や機械学習がすでに広く普及し、さらなる進化を遂げようとしている今、数理最適化の研究に求められる役割がますます重要度を増すことは間違いない。研究拠点をつくり、研究者同士が切磋琢磨することで連続最適化の分野の活性化を図るのが、このプロジェクトのねらいの一つだ。

研究拠点のもう一つの目的は、応用分野の研究者との連携を深めることだ。「応用分野の研究者は、制御や金融、都市計画などそれぞれの専門の学会に参加するのが一般的で、数理最適化に関連する学会に参加している人はあまり多くいません。交流するメリットは大きいはずですが、場が少ないのが実情です」と成島准教授は指摘する。

田中、檀准教授、成島准教授の3人は連続最適化の専門家で、数理最適化の専門家が多く集まる日本オペレーションズ・リサーチ（OR）学会で知り合った。田中は理論やモデリング、アルゴリズムに加えて応用も少々、と連続最適化の全般を広く手掛けている。大学で土木情報学を教える檀准教授は、連続最適化の分野では非線形最適化問題を解くソルバー（ソフトウェア）の開発を研究している。もともと応用数学系の学部出身という成島准教授は、連続最適化のアルゴリズム開発が専門。経営工学分野でポートフォリオ最適化や最短経路問題などのモデリングにも取り組む。

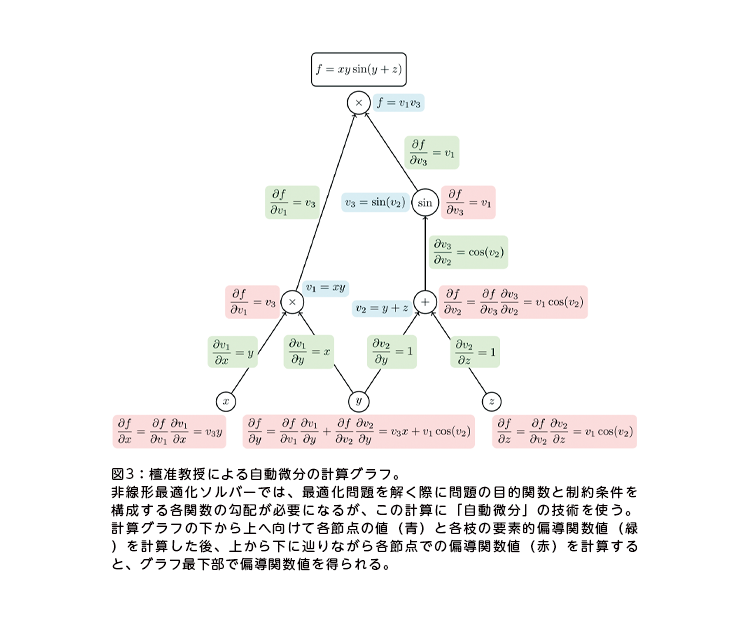
一方、豊田助教の専門は制御工学の理論だ。統数研の統計思考院に特任助教として在籍していた縁で田中と知り合い、共同研究につながった。「制御入力となる電圧などは連続量なので、制御にも連続最適化が有効ではないか。そう思い、田中准教授の統数研でのセミナーの発表を聴講したのをきっかけに、数理最適化の共同研究を始めました。最適化の専門家と議論すると、制御とは考え方が違う面も多く、発見がある。私にとってはそれがとても有意義です」と豊田助教は話す。

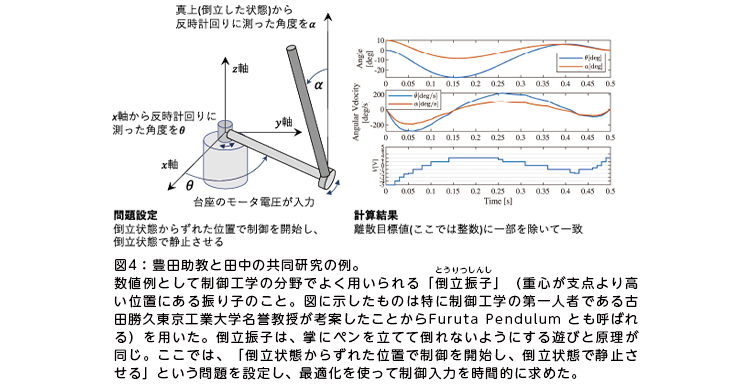
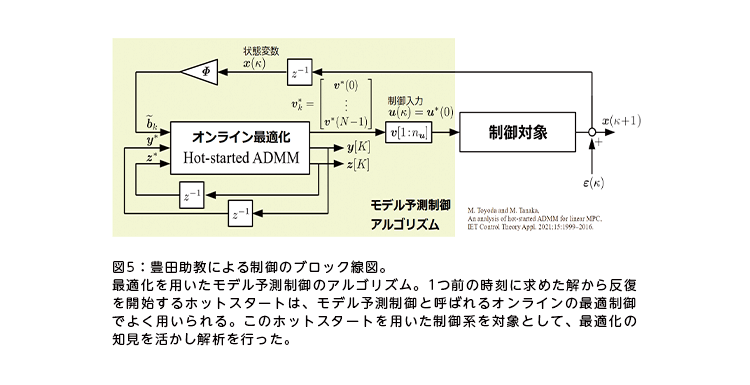
豊田助教は2021年3月に、田中との共同研究の成果を数理最適化の研究集会で発表した。この研究では、最適制御問題において制御入力を与えられた候補値のいずれかに近づけるという問題を扱い、この問題を効率よく解くアルゴリズムを提案し、その理論的性質を示した。また、数値例として具体的な制御の問題に対して提案手法を適用し、短い計算時間でよい性質をもつ制御入力を求めることに成功した。

「問題を見せたらすぐに田中先生は解き方のアイデアを教えてくれました。おかげで、最適化の知見を活かして新しいアルゴリズムを作ったり、新しい理論的な結果が得られたりしました。最適化の研究集会で発表をしたのは自分にとって初めてで、いい経験になりました」（豊田助教）。

制御分野との共同研究は国内の数理最適化コミュニティではあまり多くない。豊田助教とのコラボレーションによって、田中もまた新たな世界が拓けたという。「実際に近い問題を解いた研究はインパクトがあるので、豊田さんのように応用分野の問題を持っている人とつながりがあるのは、私にとってもありがたいこと。制御の世界ではこんな構造の問題を解く必要が生じるケースがあるのか、と気づかせてもらいました」と田中は話す。