野球などのリーグスポーツでは、シーズン中盤を過ぎた頃から、「あと何試合勝てば優勝か」あるいは「プレーオフ進出か」がファンの最大関心事になる。それを算出するのが「クリンチナンバー」だ。ルールが複雑な競技でプレーオフのように複数チームの順位が問題となる場合、クリンチは「非線形」となり、計算量は膨大になる。統計数理研究所は、ドイツの研究機関との共同研究によって、そのアルゴリズムを確立した。
セ・リーグのCS進出を巡ってマジックナンバーに食い違い

今からちょうど10年前の秋、プロ野球界で、クライマックスシリーズ(CS)への出場が決定するマジックナンバーを巡り、ちょっとした混乱が起こった。
9月12日、マスコミは一斉に巨人の出場決定を報じた。11日の試合が終わった時点でCSマジックが「1」となったからだ。ところが、実際はその時点で(2023年10月3日修正)、巨人はセントラル・リーグで3位以内に入ることが決定していたことが判明したのだ。
当時、日本のプロ野球セ・リーグには、「優勝マジック」と「CSマジック」の2種類のマジックナンバーがあった。前者は「他のチームが残り試合を全勝しても、自分のチームの優勝が確定する」と言える残り勝ち試合数を表す。つまり、「マジック1」ならば「あと1勝すれば優勝確定」であり、優勝が確定した時点で「マジック0」となる。マジックが「点灯」するのは、他の全チームに自力優勝の可能性がなくなった瞬間だ。
一方、CSマジックは、CSへの進出が決定するまでの最小勝ち試合数を表す。CSに出場できるのはリーグ戦の上位3チーム。
09年のケースで言えば、巨人が残り試合を全敗した場合の勝率と、他のチームが残り試合を全勝したときの勝率を比較し、巨人を上回ることのできないチームが3チーム以上になった時点で、巨人のCSマジックが0となる。
11日の試合終了時、5位の広島と6位の横浜は残り試合全勝でも巨人を上回ることができなくなり、3位のヤクルトと4位の阪神は残り試合を全勝すれば巨人をわずかに上回る状況となった。このため、巨人のCSマジックが1となったのである。
しかし、その時点で(2023年10月3日修正)、ヤクルトと阪神の直接対決が6試合残っており、その勝敗を加味すると、両方のチームが共に巨人を上回る可能性はなかった。巨人が4位以下になる可能性もなくなっていたことから、すでに巨人はCSマジックを0とし、CS進出を決めていたことになる。
どのメディアも、共同通信社の配信するマジックナンバー情報を基に記事を作成していたため、この食い違いが見過ごされてしまった。
最適化問題としてクリンチナンバーを解く手法で特許を取得
共同通信社は、この事態を受けて統計数理研究所に協力を依頼した。従来のCSマジックナンバーのように「あと何勝すればいいか」と上限を与える目安にとどまらず、最小の勝数を正確に与える新しい指標を模索してのことだった。
相談を受けた伊藤聡教授(現 統計数理研究所副所長)は同社と共同研究を進め、2010年にCS進出までの目安を計算する新たな指標「CSクリンチナンバー」を開発し、特許を取得。共同通信社は、各加盟メディアへの配信を開始した。
伊藤は「クリンチナンバーの算出が最も難しいのは、間違いなく日本のプロ野球でしょう。ルールが複雑なうえ、チーム間の勝率が同率の場合の取り扱いなどに、明文化されていないルールがあり、条件が非常に細分化されるからです」と話す。
しかも、優勝マジックでは1位になるための最小勝数だけを考えればいいのに対し、CSでは「3位以内」が条件になることから、点灯チームも比較の対象となるチームも複数となる。伊藤の開発したCSクリンチナンバーは、最適化手法を用いて計算の必要のないパターンを排除することで、短時間で計算できる方法だ。
クリンチナンバーの「clinch」は「決着をつける」という意味だ。ちなみにマジックナンバーは「majic word(呪文)」から派生した言葉。ビンゴゲームで、「この数字が来ますように」と祈るときの数字をマジックナンバーと呼んでいたのが、野球などのリーグスポーツにも使われるようになったという。
複雑なルールがもたらす「非線形性」の整数計画問題を解くアルゴリズム

2010年に開発したCSクリンチナンバーの計算方法は、今でも共同通信社の配信に使われている。しかし、伊藤の挑戦がそこで終わったわけではない。
「じつは開発のとき、解けない問題が一つありました。その部分を回避するために、別のさまざまな方法を組み合わせて解を求めています。計算結果は同じですが、学術的にはそれを直接解けるようにしたいと思っていたのです」と伊藤は振り返る。
そのためには「整数非線形計画問題」を解く必要があった。そこで、ドイツ・ベルリン州の研究機関「Zuse Institute Berlin(ZIB、コンラート・ツーゼ情報技術センター)」に所属する研究者で、統数研の客員でもある品野勇治教授に相談を持ちかけた。
品野は整数計画問題を含む離散最適化計算の専門家だ。2004 年に「広辞苑に収載された名詞を使ってどこまで長いしりとりを作ることができるか」という「最長しりとり問題」を整数計画問題として解き、テレビ番組「トリビアの泉」に出演したことでも知られている。
世界で初めて機械式コンピューターを開発した発明家のコンラート・ツーゼの名を冠したZIBは、計算のアルゴリズムなどコンピューター技術に特化し、最先端の研究を進めている。
この研究所の大きなテーマとなっているのが、今まで解けていなかった複雑な問題について、数理計画問題としてモデル化し、それを解くソフトウェアを開発すること。鉄道、ガス輸送、医療などさまざまな分野の課題を手がけており、それらの共通する部分を一般化したソフトウェアパッケージ「SCIP Optimization Suite(略称スキップ)」を開発している。
物流の単位は1個、1箱、1ロット…と、ほとんどの場合に整数だ。従って、世の中の最適化の課題の多くは整数計画問題に帰結する。「ただし、整数計画問題を解くには膨大な量の計算が必要。この20 年間でアルゴリズムが著しく進歩し、計算速度が1兆倍ぐらい上がってきたので、かなり解けるようになってきたところです」と品野は説明する。しかも、整数計画問題に非線形性が加わると、解析は飛躍的に複雑になるという。
SCIPには数年前、新たな機能が搭載された。それが、ガスパイプラインの設計に関連して必要となった混合整数非線形計画法(MINLP)ソルバーだ。ガスパイプライン設計の最適化問題は、管内の圧力と温度の関係などには非線形性があることから、これまで解くことができなかった難問の一つだ。
CSクリンチナンバーを直接解く問題もまた、非線形だ。「日本のプロ野球の場合、順位決定のルールが非常に複雑なので、数式で表すとA4の用紙に4ページ分にもなります」と伊藤は笑う。膨大な条件を満たすパラメーターの中から、ある関数を最大あるいは最小にするものを決める計算をしなくてはならない。2010年の時点では、この複雑さにコンピューターのアルゴリズムが追いついていなかった。
「MINLPソルバーは、まさにクリンチナンバーの問題を解くのにうってつけのソフトなのです。これを使ってどこまで解けるかやってみよう、ということになりました」と品野は説明する。
最初の数年間、二人はCSクリンチナンバーに適したモデルをひたすら検討し続けた。ようやくモデルが完成しても、今度は計算の段階で困難が待っていた。「1日に何問も解かなければいけないのに、1問を計算するのに数日かかることもありました」と品野は苦笑する。
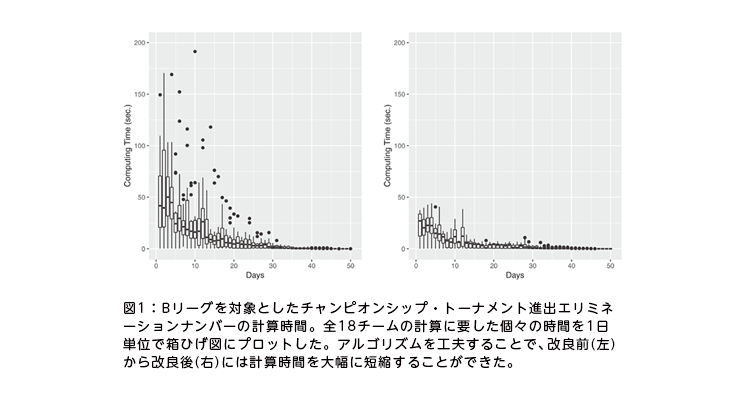
1問にかかる時間は最長でも1分以内に収めなければ、実用では使いものにならない。それ以後の研究は、アルゴリズムの改良に多くの時間を費やすことになった。
こうした苦労を乗り越え、今、ようやくアルゴリズムはほぼ完成したと言える段階に到達。計算時間も大幅に短縮した(図1)。
あらゆるリーグスポーツ、そして産業界の諸問題への展開を視野に
「整数計画問題は、汎用性が高いのが最大の魅力です」と品野は言う。今回のCSクリンチナンバーの解法も汎用化が可能で、世界中のほぼすべてのリーグスポーツに展開できる。
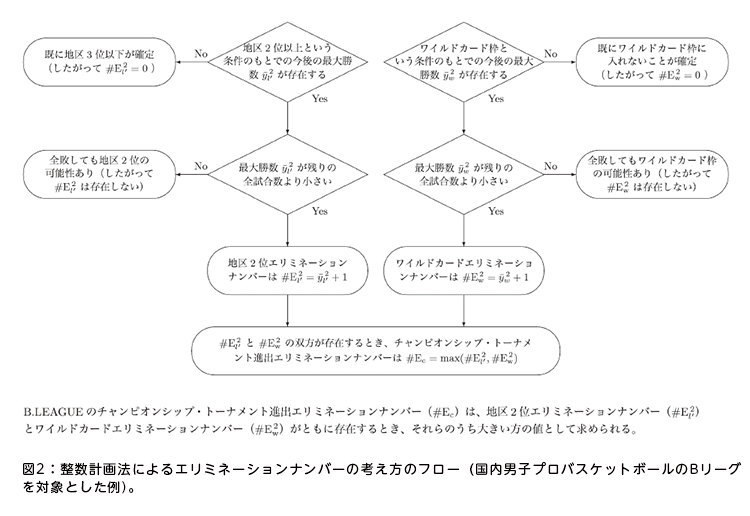
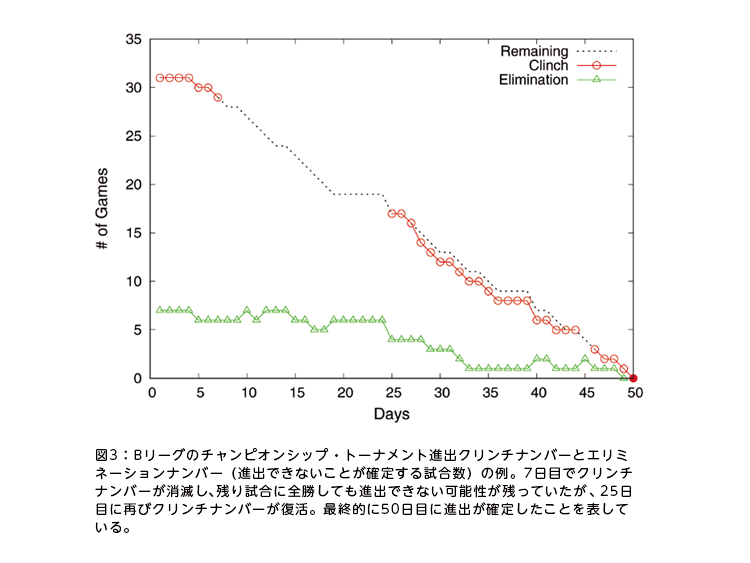
実際に、伊藤と品野は国内男子プロバスケットボール「Bリーグ」を対象としてクリンチナンバーの算出プログラムを完成させ、2018年秋に論文を発表した(図2、3)。また、統数研に留学している台湾人学生とともに、台湾のプロ野球のルールを踏まえたクリンチナンバー算出法を理論化。現地での論文発表も実現した。
さらに、伊藤は「このモデルを使って例えば、そのスポーツのシーズン中の終盤の時期、野球なら9月頃に最も盛り上がるようなルール改正を提案することもできます。スポーツをより面白くするためにも役立つでしょう」と話す。
この問題に取り組む意義はそれだけではない。整数計画化問題は、産業界が抱える最適化問題のカギを握る。その計算手法の進化に貢献することで、数理研究と産業界の連携を強化することにもつながるはずだ。
統数研とZIBは、九州大学マス・フォア・インダストリ研究所(IMI)と三者間で学術協定を結んでいる。日本とドイツの産業界を含めた連携を推進することが目的だ。2017 年から毎年ワークショップを開催しており、その第2回で、伊藤と品野は整数計画に基づくクリンチナンバー、エリミネーションナンバーの計算について発表した(図4)。
伊藤は統数研の副所長として「産業界との連携を深めることは、産業発展を下支えすることにつながると同時に、研究機関にとって外部資金獲得の機会ともなる。今後も積極的な展開を目指していきます」と抱負を語った。

(広報室)
