dm, a Dirichlet Mixtures tool.
Daichi Mochihashi
NTT Communication Science Laboratories
$Id: dm.html,v 1.6 2006/12/27 11:40:11 daiti-m Exp $
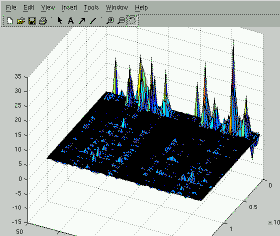
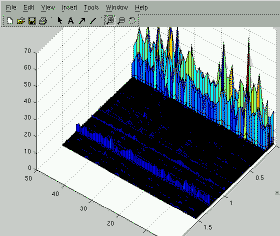
Dirichlet Mixtures (DM) is a text model proposed by
Yamamoto et al. [1][2][3]
and considered an extension to the model for amino acids [4].
As opposed to the 20 amino acids,
natural language has typically a huge number of words,
which precludes ordinary Newton-Raphson parameter estimation formulae
in [4].
Strictly speaking, DM is a shorthand for a
"Mixture of Dirichlet-Multinomial (Polya) distribution of unigrams".
DM works on the word simplex directly: so there is no need to use (VB-)EM
procedure, and the posterior is derived in closed form
(this property is perhaps first described by Antoniak (1974)).
Generally, DM yields a lower perplexity than LDA in document modeling.
Under DM, document \mathbf{w} = w_1 w_2 .. w_N is generated as follows.
- Draw m ~ Mult(\lambda).
- Draw p ~ Dir(\alpha_{m}).
- for n = 1 .. N,
- Draw w_n ~ Mult(p).
Steps 2 and 3 are essentially a Polya urn scheme:
Therefore,
this process places a mixture of Dirichlet prior on the word simplex
directly.
Download
- dm-0.1.tar.gz
- Implements a simple EM-(quasi)Newton procedure described in [1,2].
- dm-0.2.tar.gz
- Implements the Reversing EM (Minka 1999) procedure of Bayesian
hierarchical smoothing of DM, described in [3].
Usage
% dm -h
dm, a Dirichlet Mixture toolkit.
Copyright (C) 2004 Daichi Mochihashi, All rights reserved.
$Id: dm.c,v 1.2 2005/05/31 12:55:56 daiti-m Exp $
usage: dm -M mixtures [-I iter] [-E epsilon] train model
For example,
% dm -M 50 train model
yields two files of DM parameters: "model.lamba" and "model.alphas".
"model.lambda" is a 1 x M vector of \lambda, and
"model.alphas" is a L x M matrix of \alpha_{1 .. M} of the Dirichlet Mixture.
(Here, M is a number of mixtures (in the above example, 50), and
L is the number of words in the lexicon.)
Both files can be loaded by MATLAB, or can be used by other programs.
"train" is a data file representing bag of words: this is of the same format as
lda.
References
- [1] Dirichlet Mixtures in Text Modeling.
Mikio Yamamoto, Kugatsu Sadamitsu.
CS Technical Report CS-TR-05-1, University of Tsukuba, 2005.
[PDF]
- [2] Context modeling using Dirichlet mixtures and its applications to
language models.
Mikio Yamamoto, Kugatsu Sadamitsu, Takuya Mishina,
IPSJ 2003-SLP-48, 2003.
[PDF] (in Japanese)
- [3] A smoothing method for parameters of Dirichlet mixtures
using hierarchical Bayesian models.
Kugatsu Sadamitsu, Yuusuke Machitori, Mikio Yamamoto,
IPSJ 2004-SLP-53, 2004 Oct.
[PDF] (in Japanese)
- [4] Dirichlet Mixtures: A Method for Improving Detection of Weak but Significant Protein Sequence Homology.
Sjolander, K., Karplus, K., Brown, M., Hughey, R., Krogh, A., Mian, I.S., and Haussler, D.
Computing Applications in the Biosciences, 12(4): 327-345, 1996.
[UCSC]
-
- [5] Mixtures of Dirichlet Processes with Applications to Bayesian
Nonparametric Problems.
Charles E. Antoniak, Annals of Statistics, vol.2, no.6,
pp.1152-1174, 1974.
Figures:
Right: >> surf(alphas);
Left: >> surf(alphas-repmat(mean(alphas,2),1,size(alphas,2)));
daichi <at> cslab.kecl.ntt.co.jp
Last modified: Tue Apr 10 10:30:44 2007

